Глава двенадцатая
ЭЛЕКТРОПРИВОД, ВЫБОР ДВИГАТЕЛЯ, АППАРАТУРА УПРАВЛЕНИЯ,
ЭЛЕКТРОСНАБЖЕНИЕ, ВОПРОСЫ ТЕХНИКИ БЕЗОПАСНОСТИ
12.2. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРОПРИВОДАХ
Переходным процессом называется процесс перехода электропривода от одного установившегося состояния к другому, когда одновременно изменяются скорость, момент и ток двигателя, а также скорость и моменты всех звеньев кинематической цепи, соединяющей двигатель с рабочим органом механизма.
К переходным процессам относятся пуск, торможение и реверс электропривода, переход с одной скорости на другую, а также процессы, вызванные изменениями момента на валу двигателя, изменением напряжения сети. Характер протекания и длительность переходного процесса в ряде производственных механизмов определяют производительность, особенно когда длительность рабочего цикла соизмерима с временем разгона и торможения.
Кроме того, потери энергии в двигателе при пуске и торможении могут оказаться соизмеримыми с потерями в установившихся режимах. Поэтому при определении мощности двигателя необходимо учитывать потери при пуске и торможении, особенно когда число пусков и торможений в час относительно велико.
Характер и длительность переходного процесса определяются моментом двигателя, моментами сил сопротивления (трения, резания, деформации и т. д.), массами и моментами инерции движущихся тел. Зависимости n, М, I от времени и продолжительность переходного процесса можно определить с помощью известного из механики уравнения движения. Для поступательного движущегося тела
F - Fc = mdv/dt.
Для вращающегося тела
М - Mc = J dω/dt.
В формулах (12.1) и (12.2) приняты следующие обозначения: F, М — движущая сила и движущий момент, Н, Н•м; Fc, Мс — сила и момент сопротивления, Н, Н•м; т, J — масса и момент инерции тела, кг, кг•м2; v, ω, t — скорость, угловая скорость и время, м/с, рад/с, с.
Уравнения движения соответствуют одному поступательно движущемуся или вращающемуся телу. Любой, даже самый простейший производственный механизм, например изображенный на рис. 12.1, состоит не из одного, а из нескольких движущихся или вращающихся с различными частотами тел (шестерен, валов, шкивов и т. д.). Поэтому при расчете переходных процессов электроприводов потребовалось бы составить и совместно решить столько уравнений, сколько звеньев с различными скоростями имеет механизм. Для упрощения задачи все моменты инерции, моменты сил сопротивления и движущие моменты приводят к одной скорости — обычно к скорости вала двигателя; в результате этого все звенья механизма заменяют одним эквивалентным звеном, для которого составляют и затем решают одно уравнение движения. Динамические свойства эквивалентного звена будут такими же, как и механизма, если:
а) кинетическая энергия эквивалентного звена равна кинетической энергии всех звеньев механизма;
б) мощности на валу эквивалентного звена, обусловленные движущим моментом и моментами сил сопротивлений, те же, что и соответствующие мощности, передаваемые звеньями механизма.
На основании этих условий для системы, состоящей из k звеньев, можно написать
| Jэкω2эк | = Jд | ωд2 | + J1 | ω12 | + ... + Jk | ωk2 | . |
| 2 | 2 | 2 | 2 |
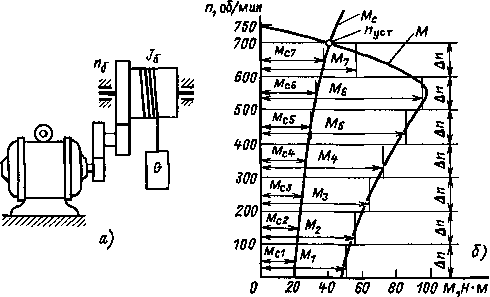 |
Рис. 12.1. Кинематическая схема механизма (а); пояснения к графо- аналитическому методу расчета времени переходного процесса (б) |
Разделив почленно на ωэ, получим
| Jэк = Jд( | ωд | )2 + J1( | ω1 | )2 + ... + Jk( | ωk | )2, |
| ωэк | ωэк | ωэк |
Если скорость эквивалентного звена равна скорости двигателя, то
| Jэк = Jд+ J1( | ω1 | )2 +... + Jk( | ωk | )2, |
| ωд | ωд |
Эквивалентный момент инерции Jэк обычно обозначают Jи называют моментом инерции всех звеньев механизма, включая и момент инерции двигателя.
Момент сил сопротивления, приведенный к валу двигателя, с учетом КПД механизма для случая передачи энергии от двигателя к механизму определяется из соотношения
Рс,пр = Рс/η или Мс,прωпр = М'сω'с/η.
Отсюда
| Мс,пр = М'с | ωс | 1 | = Мс, | |
| ωд | η |
где Мс,пр — момент сил сопротивления, приведенный к валу двигателя, имеющего угловую скорость ωд; М'с — момент сил сопротивления звена, имеющего угловую скорость ω'с; η— КПД передачи.
Уравнение движения эквивалентного звена для двигательного режима работы и реактивного момента сил сопротивления (момент трения, резания и т. п.) будет иметь вид (12.2), где М — момент, развиваемый двигателем; J— момент инерции всех звеньев; Мс — момент сил сопротивления на валу двигателя.
Пример 12.1. Двигатель через систему шестерен приводит в движение барабан (рис. 12.1, а). Частота вращения двигателя n= 1000 об/мин, частота вращения барабана n = 100 об/мин. Момент сил сопротивления на валу барабана Мс = 400 Н • м, момент инерции барабана Jб = 250 кг • м2.
Определить приведенные к валу двигателя момент инерции барабана и момент сил сопротивления, если КПД передачи η = 0,8.
Решение. Момент инерции барабана, приведенный к валу двигателя,
| Jб, пр = Jб ( | ωб | )2 = Jб ( | nб | )2 = 250( | 100 | )2 = 2,5 кг • м2. |
| ω | n | 1000 |
Момент сил сопротивления, приведенный к валу двигателя,
| Мс = М'с | ωб | 1 | = Мс | nб | 1 | = 400 | 100 | 1 | = 50 Н • м. | |||
| ω | η | n | η | 1000 | 0,8 |
