Глава четвертая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
4.6. ПЕРЕХОДНЫЙ ПРОЦЕСС В ЦЕПИ ПРИ ИЗМЕНЕНИИ ЕЕ ПАРАМЕТРОВ
Рассмотрим переходный процесс в цепи, вызванный изменением ее параметров, например изменением сопротивления в одном из участков цепи, изображенной на рис. 4.6, а.
До замыкания выключателя ток в цепи
| Iнач = | U | . |
| r + r1 |
После замыкания выключателя
Iуст = U/r.
Таким образом, при замыкании выключателя в цепи возникает переходный процесс, в течение которого ток изменяется от Iнач до Iуст.
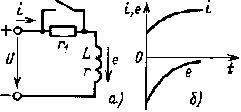 |
| Рис. 4.6. Зависимости i(t), e(t)(б) при изменении параметров цепи r, L(а) |
Уравнение цепи, составленное по второму закону Кирхгофа, имеет вид
Ldi/dt + ir = U.
Решением уравнения без правой части (для свободного тока)
Ldiсв /dt + iсв r = 0
iсв = Аеpt.
Из характеристического уравнения Lp + r = 0 определяют показатель степени р:
| р = - | r | = - | 1 | ; |
| L | T |
Общий ток в цепи
i = iycт + Ae-t/T,
При t = 0+
| i = Iнач = | U | и А = | U | - | U | ; |
| r + r1 | r + r1 | r |
После подстановки А в (4.37) получим уравнение для тока в переходный период:
| i = | U | + ( | U | - | U | )е-t/T. |
| r | r + r1 | r |
Подставив i из (4.38) в (4,36), получим выражение ЭДС
| e = ( | Ur | - U)е-t/T. |
| r + r1 |
На рис. 4.6, б изображены графики i и е переходного процесса в цепи рис. 4.6, а.
Пример 43. Определить начальное значение ЭДС е в индуктивности цепи, изображенной на рис. 4.6, а, при замыкании выключателя, шунтирующего резистор r1.
Параметры цепи: r = 1000 Ом, r1 = 4000 Ом, U = 200 В.
Решение. До замыкания выключателя ток в цепи
| I = | U | = | 200 | = 0,04 А. |
| r + r1 | 1000+4000 |
После замыкания выключателя ток должен сохранить прежнее значение при t = 0+, тогда
I = Iнач - 0,04 А.
Из уравнения, составленного по второму закону Кирхгофа, определяем начальное значение ЭДС е:
e = ir - U;
е = Енач = Iнач r - U = 0,04•1000 - 200 = - 160 В.
