§ 78. Максимальная величина крутящего момента

[an error occurred while processing this directive]

Все справочники Предисловие

Введение

Введение

§ 1. Краткий исторический обзор § 2. Опыт Фарадея § 3. Принцип действия современного асинхронного двигателя § 4. Вращающееся магнитное поле (двухфазное) § 5. Вращающееся магнитное поле, создаваемое трехфазным током

Глава I

Глава I. Обмотки асинхронных двигателей

§ 6. Классификация § 7. Катушечные обмотки § 8. Связь между числом полюсов и числом шпуль катушечной обмотки § 9. Катушечная обмотка при нечетном числе пар полюсов (р) § 10. Катушечная обмотка с дробным числом пазов на полюс и фазу (q) § 11. Схемы двухплоскостных и трехплоскостных катушечных обмоток § 12. Катушечная обмотка для разъемного статора § 13. Симметричная катушечная обмотка § 14. Катушечная обмотка с "короткими" шпулями § 15. Влияние укорочения шага обмотки на форму кривой индуктиро ванной э. д. с. § 16. Обмотки с укороченным шагом § 17. Трехфазная двухслойная обмотка (так называемая "американская") § 18. Фазная стержневая обмотка ротора § 19. Разрезные обмотки постоянного тока § 20. Способы намотки § 21. Открытые пазы § 22. Открытые и полузакрытые пазы § 23. Американская и европейская системы изоляции обмоток § 24. Изоляция паза

Глава II

Глава II. Роторные обмотки

§ 25. Классификация § 26. Беличье колесо § 27. Роторная обмотка с короткозамкнутыми секциями § 28. "Комбинированные" роторные обмотки

Глава III

Глава III. Обмоточный коэфициент

§ 29. Понятие об обмоточном коэфициенте § 30. Общее выражение для наведенной э. д. с § 31. Влияние характера размещения обмотки в пазах на величину обмоточного коэфициента "распределения" § 32. Общая формула для нахождения величины обмоточного коэфициента „распределения"kp § 33. Обмоточный коэфициент „распределения" гладкой обмотки § 34. Обмоточный коэфициент „распределения" многофазной обмотки § 35. Обмоточные коэфициенты высших гармоник

Глава IV

Глава IV. М. д. с. обмоток асинхронного двигателя

§ 36. Кривая м. д. с. однофазной обмотки § 37. Разложение в ряд Фурье кривой м. д. с. § 38. Общее выражение для нахождения величин м. д. с. в любой момент времени (t) и в любой точке (х) окружности статора § 39. Кривая м. д. с. для трехфазной обмотки § 40. Уравнение м. д. с. вращающегося поля для трехфазной обмотки § 41. М. д. с, создаваемая обмотками с большим числом пазов на полюс и фазу (q) § 42. М. д. с. равномерно распределенной трехфазной обмотки § 43. Многоугольник Гергеса

Глава V

Глава V. Э. д. с, индуктированные в обмотках асинхронного двигателя

§ 44. Магнитные потоки в асинхронном двигателе. § 45. Э. д. с, индуктированные потоками рассеяния ФS1 и ФS2 § 46. Э. д. с, наводимые потоком Ф

Глава VI

Глава VI. Асинхронный двигатель как трансформатор

§ 47. Ток ротора § 48. Изменение величины магнитного потока Ф. § 49. Величина потока Ф § 50. Связь между ампервитками статора (AW1) и ротора (AW2) § 51. Диаграмма ампервитков § 52. Диаграмма токов § 53. Коэфициент трансформации § 54. "Приведенные" величины § 55. Аналогия между асинхронным двигателем и трансформатором § 56. Векторная диаграмма неподвижного двигателя

Глава VII

Глава VII. Явления, происходящие во вращающемся двигателе

§ 57. Общее выражение крутящего момента § 58. Диаграмма ампервитков и токов вращающегося двигателя § 59. Скольжение и частота в роторе § 60. Зависимость между скольжением и э. д. с. фазного ротора § 61. Ток фазного ротора в функции скольжения двигателя § 62. Эквивалентная схема для роторного тока § 63. Два вида векторной диаграммы э. д. с. и тока ротора § 64. Полная векторная диаграмма вращающегося двигателя § 65. Векторная диаграмма э. д. с. и потоков

Глава VIII

Глава VIII. Ротор в виде беличьей обмотки (короткозамкнутый ротор)

§ 66. Надежность беличьего ротора § 67. Электродвижущие силы и токи в беличьей обмотке ротора

Глава IX

Глава IX. Асинхронный двигатель как универсальный преобразователь

§ 68. Асинхронный двигатель как универсальный преобразователь § 69. „Энергетическая" диаграмма § 70. Мощность, подводимая к ротору вращающимся магнитным потоком (PS) § 71. Механическая аналогия

Глава X

Глава X. Крутящий момент

§ 72. Полное выражение крутящего момента § 73. Величина крутящего момента, выраженная в „синхронных ваттах" (PS) § 74. Связь между величиной крутящего момента и джоулевыми потерями в обмотке ротора § 75. Пусковой момент § 76. Зависимость величины крутящего момента от величины магнитного потока § 77. Влияние напряжения U на величину крутящего момента § 78. Максимальная величина крутящего момента § 79. Влияние величины активного сопротивления цепи ротора на величину пускового момента § 80. Форма кривой крутящего момента § 81. Связь между Mmax , M и скольжением s § 82. Крутящий момент при малых скольжениях § 83. Зависимость крутящего момента от частоты f1тока, питающего двигатель, и омического сопротивления цепи ротора r2 § 84. Кривая начального момента вращения в функции сопротивления цепи ротора § 85. „Гистерезисный" момент § 86. Местные магнитные потоки и явления „прилипания" § 87. Мощность ротора (Р'2) и скольжение (s) § 88. Зубцовые поля и влияние их на форму кривой крутящего момента и на шум машины

§ 89. Влияние скоса пазов ротора на высшие гармоники

Глава XI

Глава XI. Потери и к. п. д.

§ 90. Потери в асинхронном двигателе § 91. Потери холостого хода § 92. Перемагничивание железного цилиндра, вращающегося в постоянном магнитном поле § 93. Перемагничивание железного ротора вращающимся потоком § 94. Потери на гистерезис в статоре асинхронного двигателя § 95. Формула для подсчета потерь на гистерезис § 96. Вихревые токи, появляющиеся в железе ротора при его вращении § 97. Потери на токи Фуко в железе статора § 98. Формулы для подсчета потерь на токи Фуко § 99. Формула для подсчета суммарных потерь железа § 100. Потери на гистерезис и вихревые токи в сердечнике статора (индекс s) § 101. Потери на гистерезис и вихревые токи в зубцах статора (индекс z) § 102. Влияние механической обработки на потери в железе § 103. Потери в железе ротора § 104. Добавочные потери в железе § 105. Потери в болтах § 106. Учет дополнительных потерь § 107. Нагрузочные потери § 108. Вихревые потери в меди статора и ротора § 109. Экспериментальное исследование явления „вытеснения тока" (Опыты К. И. Шенфера и А. И. Москвитина) § 110. Форма кривых токов, текущих в проводах ротора §111. Механические потери § 112. Потери на трение в подшипниках § 113. Потери на трение щеток о контактные кольца § 114. Вентиляционные потери § 115. Коэфициент полезного действия § 116. Кривые к. п. д

Глава XII

Глава XII. Нагревание машин

§ 117. Влияние нагревания на продолжительность службы изоляции § 118. Изменение температуры нагрева электрической машины в функции времени § 119. Классификация изолирующих материалов § 120. Допускаемый нагрев машины § 121. Эмпирические формулы для подсчета перегрева машины § 122. Общее выражение для нахождения повышения температуры § 123. Повышение температуры железа статора § 124. Влияние вентиляционных прослоек на величину удельной поверхности охлаждения § 125. Нагрев меди статора § 126. Нагрев меди ротора § 127. Теплопроводность изолирующих и активных материалов § 128. Расчет вентилятора § 129. Машины „закрытого типа"

Глава XIII

Глава XIII. Вывод круговой диаграммы

§ 130. Опыт § 131. Краткая история § 132. Простейшая цепь, имеющая круговую диаграмму § 133. Другой вид векторной диаграммы асинхронного двигателя § 134. Эквивалентная схема для векторной диаграммы согласно фиг. 143 (левый чертеж) § 135. Упрощенная схема замещения § 136. Токи короткого замыкания I2k и I2ki § 137. Доказательство существования круговой диаграммы для полной схемы замещения § 138. Поправка на падение напряжения в статоре I0x1 § 139. Другой способ доказательства существования круговой диаграммы § 140. Опыт холостого хода и короткого замыкания § 141. Влияние магнитного насыщения на очертания „круговой диаграммы"

Глава XIV

Глава XIV. Пользование круговой диаграммой

§ 142. Джоулевы потери на круговой диаграмме § 143. Подводимая мощность (P1) § 144. Полезная мощность (Р2) § 145. Крутящий момент § 146. Физический смысл точки К∞ § 147. Физический смысл точки К § 148. Коэфициент мощности (cos φ) § 149. Скольжение § 150. Построение круговой диаграммы § 151. Максимальная величина коэфициента мощности

Глава XV

Глава XV. Асинхронная машина как генератор

§ 152. Асинхронная машина как генератор § 153. Параллельная работа асинхронного генератора с сетью § 154. Самовозбуждение асинхронного генератора § 155. Асинхронная машина как электротормоз (вращение "против поля")

Глава XVI

Глава XVI. Пуск в ход многофазных асинхронных двигателей
(при фазной обмотке ротора)

§ 156. Способ пускового реостата § 157. Крутящий момент при неподвижном двигателе § 158. Величина крутящего момента при вращении двигателя § 159. Пусковые реостаты § 160. Включение индуктивного сопротивления в цепь ротора § 161. Включение в цепь ротора реостата через посредство трансформатора (метод "третичных" токов Рюденберга) § 162. Метод дроссельной катушки с массивным железным сердечником § 163. Нестационарные процессы, происходящие в асинхронном двигателе в момент включения его обмоток на сеть § 164. Пусковые свойства двигателей с беличьим ротором

Глава XVII

Глава XVII. Пуск в ход многофазных асинхронных двигателей
(при короткозамкнутой обмотке ротора)

§ 165. Пуск в ход по методу пересоединения со звезды на треугольник § 166. Работа асинхронного двигателя при соединении его статора в звезду и треугольник § 167. Метод автотрансформатора § 168. Двигатель с двойным статором Бушеро § 169. Двигатель Брункена (Brunken) § 170. Двигатель с двойной беличьей клеткой ротора § 171. Кривая крутящего момента двигателя с двойной клеткой § 172. Алюминиевая обмотка ротора. Глубокие пазы § 173. Другие модификации ротора Бушеро § 174. Нагрев пусковой клетки § 175. Ротор в виде массивного железного цилиндра § 176. Пуск в ход больших асинхронных двигателей с короткозамкнутым ротором § 177. Двигатель Рихтера

Глава XVIII

Глава XVIII. Безреостатный пуск в ход асинхронных двигателей с фазным ротором по методу "противосоединения"

§ 178. Схемы Гергеса § 179. Токи ротора при второй схеме противосоединения (шестифазной) § 180. Величина коэфициента взаимоиндукции § 181. Коэфициент самоиндукции одной фазы ротора при его рабочем соединении § 182. Сдвиг фаз в роторе

Глава XIX

Глава XIX. Другие методы противосоединения. Короткозамкнутый двигатель как наиболее распространенный тип

§ 183. Описание схемы противосоединения, предложенной автором § 184. Переключение обмотки ротора в рабочее положение § 185. Пуск в ход по методу противосоединения обмоток статора(Б. П. Апарова) § 186. Коэфициент эффективности пуска § 187. Сопоставление трех типов двигателей с короткозамкнутым ротором § 188. Наиболее распространенный тип асинхронного двигателя с безреостатным пуском

Глава XX

Глава XX. Краткая теория ротора с двойной беличьей клеткой и с глубоким пазом

§ 189. Схема замещения для двигателя с двойной клеткой § 190. Токи в двойной клетке § 191. Отношение токов IА/IВ в функции скольжения § 192. Векторная диаграмма э. д. с. и токов в роторе Бушеро § 193. Сопротивления клеток ротора Бушеро § 194. Зависимость активного и реактивного сопротивления ротора Бушеро от скольжения § 195. Режим малых скольжений § 196. Режим больших скольжений § 197. Круги диаграммы тока двигателя с двойным беличьим ротором § 198. Полная диаграмма тока двигателя с двойным беличьим ротором § 199. Сопоставление свойств двигателей Бушеро и с глубоким пазом § 200. Двигатель с глубоким пазом

Глава XXI

Глава XXI. Однофазные асинхронные двигатели. Теория вращающихся в противоположные стороны полей

§ 201. Общие свойства § 202. „Прямое поле" и „инверсное" поле § 203. Крутящий момент однофазного двигателя § 204. Кривые тока в роторе однофазного асинхронного двигателя § 205. Два спаренных многофазных асинхронных двигателя, магнитные потоки которых вращаются в противоположные стороны § 206. Крутящий момент агрегата, описанного в предыдущем параграфе § 207. Кривые момента однофазного асинхронного двигателя

Глава XXII

Глава XXII. Однофазные асинхронные двигатели. Теория „поперечного" поля

§ 208. Потоки в статоре однофазного асинхронного двигателя при неподвижном и вращающемся роторе § 209. Эллиптическое вращающееся поле

Глава XXIII

Глава XXIII. Системы однофазных асинхронных двигателей

§ 210. Начальный момент однофазного двигателя § 211. Метод Корсепиуса (Korsepius) § 212. Двигатель Пунга (Punga) § 213. Схемы Тесла и Штейнметца (Tesla и Steinmetz) § 214. Конденсаторные асинхронные двигатели

Глава XXIV

Глава XXIV. Регулирование скорости асинхронных двигателей
по методу изменения числа оборотов в минуту вращающегося поля

§ 215. Скорость вращения магнитного потока § 216. Двигатель с двойной обмоткой в статоре § 217. Переключение обмотки на другое число полюсов § 218. Асинхронный двигатель с двойным ротором

Глава XXV

Глава XXV. Каскадное соединение двух асинхронных двигателей

§ 219. Регулирование скорости асинхронного двигателя путем включения в цепь ротора реостата § 220. Каскадное соединение двух асинхронных двигателей § 221. Скорость каскадного агрегата § 222. Распределение мощности между машинами каскадного агрегата § 223. Эквивалентная схема для каскадного соединения § 224. Ток холостого хода в статоре двигателя I § 225. Ток, текущий в статоре двигателя I при неподвижном агрегате § 226. Коэфициент мощности при каскадных схемах § 227. Явление Гергеса § 228. Явления, происходящие при каскадном соединении асинхронных двигателей с однофазным ротором § 229. Практическое значение схемы § 230. Каскадное соединение асинхронных двигателей с переключением числа полюсов § 231. Обзорная таблица каскадных схем § 232. Двухмоторная схема (для подъемников) § 233. Регулирование скорости по методу инверсного поля

Глава XXVI

Глава XXVI. Каскадное соединение асинхронных двигателей с коллекторными машинами

§ 234. Краткая история § 235. Краткий обзор схем соединения § 236. Каскадное соединение асинхронного двигателя с машинами постоянного тока § 237. Схема Кремера с шестифазным конвертором

а) Устойчивость работы схемы Кремера б) Схема Кремера с вольтодобавочной машиной

§ 238. Схема Шербиуса с машинами постоянного тока § 239. Различные виды каскадных соединений § 240. Каскадное соединение асинхронного двигателя с коллекторным при непосредственном механическом соединении (схема Кремера) § 241. Мощность каскадного агрегата по схеме Кремера § 242. Влияние характера возбуждения вспомогательного двигателя на работу агрегата § 243. Регулирование скорости при каскадном соединении асинхронного двигателя с шунтовым коллекторным двигателем § 244. Описание схемы Шербиуса § 245. Действие схемы § 246. „Энергетическая" диаграмма схемы Кремера § 247. „Энергетическая" диаграмма схемы Шербиуса § 248. Регулирование скорости ниже синхронной при схеме Шербиуса § 249. Сверхсинхронная скорость § 250. Переход через синхронизм § 251. Схема каскадного соединения, при которой возможен плавныйпереход главного двигателя через синхронную скорость

Глава XXVII

Глава XXVII. Компенсаторы сдвига фаз

§ 252. Компенсаторы сдвига фаз с самовозбуждением § 253. Компенсатор Шербиуса § 254. Работа компенсатора с самовозбуждением при разных нагрузках главного двигателя § 255. Компенсаторы шунтового возбуждения

Глава XXVIII

Глава XXVIII. Компенсированные асинхронные двигатели

§ 256. Двигатель Гейланда (Heyland) завода Бергмана (Bergmann)

Глава XXIX

Глава XXIX. Синхронно-индукционные двигатели

§ 257. Различные методы улучшения cosφв асинхронных двигателях § 258. Синхронно-индукционные двигатели § 259. Круговая диаграмма синхронного индукционного двигателя § 260. Различные способы соединения обмотки ротора с возбудителем § 261. Синхронно-индукционный двигатель с автоматическим регулированием cos φ § 262. Индукционная машина двойного питания

Глава XXX

Глава XXX. Нестационарные процессы, происходящие в асинхронном двигателе при переходных режимах

§ 263. Внезапное включение на сеть асинхронного двигателя при разомкнутом роторе § 264. Внезапное включение статора асинхронного двигателя на сеть при закороченном роторе § 265. „Бросок" тока при включении на сеть магнитно-насыщенного статора асинхронного двигателя § 266. Перенапряжения в обмотках асинхронных двигателей

Глава XXXI

Глава XXXI. Нормальные свойства асинхронных машин

§ 267. Нормальные свойства асинхронных машин § 268. Вес машины § 269. Серии асинхронных двигателей, построенных советскими заводами

Глава XXXII

Глава XXXII. Расчет асинхронного двигателя

§ 270. О математической неопределенности расчета электрических машин § 271. Расчетные варианты § 272. Главные размеры машины § 273. "Длинные" и "короткие" машины § 274. Расчетная длина ( li ) § 275. Коэфициент формы кривой поля ( αi ) § 276. Величина магнитного потока § 277. Основное уравнение § 278. Физический смысл постоянной С; удельное тяговое усилие § 279. Исследование основного уравнения § 280. Влияние Вl и AS на размеры машины § 281. Влияние числа оборотов в минуту n1 § 282. Машинная постоянная § 283. Влияние выбора плотности тока на размеры машины § 284. Связь между величиной полюсного деления и мощностью машины § 285. Влияние быстроходности, величины Вl и δ на ток холостого хода § 286. Выбор величины воздушного зазора (δ) § 287. Пример

Глава XXXIII

Глава XXXIII. Железо и обмотки статора и ротора

§ 288. Расчет обмотки статора § 289. Число пазов статора и объем тока § 290. Связь между объемом тока Iп и линейной нагрузкой AS § 291. Число пазов на полюс и фазу в статоре (q1) § 292. Ход расчета зубцов статора § 293. Ширина зубцов и пазов статора § 294. Очертание зубцов § 295. Выбор числа витков одной фазы w2 роторной обмотки § 296. Число пазов в роторе (Z2) § 297. Ток в фазе обмотки ротора § 298. Сечение проводов фазной обмотки ротора § 299. Расчет пазов и зубцов ротора § 300. Глубина паза hn § 301. Величина магнитного потока § 302. Определение высоты железного сердечника статора и ротора § 303. Ротор с беличьей обмоткой § 304. Размеры роторных контактных колец и щеток

Глава XXXIV

Глава XXXIV. Расчет магнитной цепи

§ 305. Величина тока холостого хода § 306. Участки магнитной цепи асинхронного двигателя § 307. Нахождение ампервитков для зубцов статора (АWzs) § 308. Ампервитки для зубцов ротора (АWzr) § 309. Ампервитки для воздушного зазора (АWl) § 310. Ампервитки в сердечнике статора и ротора §311. Суммарные ампервитки

Глава XXXV

Глава XXXV. Ток короткого замыкания

§ 312. Ток короткого замыкания § 313. Активное сопротивление обмотки статора § 314. Активное сопротивление фазной обмотки ротора § 315. Приведенная величина активного сопротивления фазной обмотки ротора § 316. Реактивное сопротивление обмотки статора и ротора § 317. Удельная магнитная проводимость паза § 318. Активное и реактивное сопротивления обмотки в виде беличьего колеса § 319. Приведенные значения активного и реактивного сопротивления обмотки ротора в виде беличьего колеса § 320. Другое выражение приведенного реактивного сопротивления беличьей обмотки

Глава XXXVI

Глава XXXVI. Магнитные потоки рассеяния

§ 321. Потоки рассеяния в разных частях секции § 322. Магнитная проводимость паза λп § 323. Удельная магнитная проводимость потока рассеяния между головками зубцов (λz) § 324. Удельная магнитная проводимость потока рассеяния лобовых частей обмотки (λs) § 325. Расчет рассеяния торцевых или лобовых частей обмоток § 326. Суммарная удельная проводимость (λ) § 327. Влияние укорочения шага в двухслойных ("американских") обмотках на величину λ § 328. Приведенный реактанц обмотки ротора в виде беличьего колеса

Глава XXXVII

Глава XXXVII. Конструкция асинхронных машин

§ 329. Общий вид § 330. Конструкция ротора § 331. Приспособление для короткого замыкания § 332. Асинхронный двигатель сварной конструкции § 333. Двигатель с независимой вентиляцией § 334. Двигатель для центрифуги § 335. Новый тип двигателя для работы под водой § 336. Системы вентиляции § 337. Ротор с увеличенным активным сопротивлением § 338. Асинхронные двигатели производства советских заводов § 339. Двигатели типа Бушеро и с глубоким пазом производства советских заводов § 340. Некоторые технические данные, касающиеся асинхронных двигателей советского производства

Глава XXXVIII

Глава XXXVIII. Примерные расчеты

§ 341. Задание § 342. Задание

Обозначения

Оглавление

ГЛАВА X
КРУТЯЩИЙ МОМЕНТ

§ 78. Максимальная величина крутящего момента.

Найдем величину скольжения sm, при котором мотор развивает максимальный момент Ps = Psmax.

Для этой цели знаменатель выражения (77,1) продиференцируем по s и приравняем результат нулю

r12 + r'22/s2 + (x1 + х'2)2 = 0.

Отсюда найдем искомую величину

(77.3)

s = sm =	r'2	.
	√r12 +(x1 + x'2)2

Полагая для упрощения r1≈ 0, найдем

(77.4)

sm ≈	r'2	.
	x1 + x'2

Подставив в формулу для крутящего момента выражение для sm, найдем величину максимального момента вращения в "синхронных ваттах":

(77.5)

Psmax =	mU2	.
	2[r1 + √r12 +(x1 + x'2)2]2

Полагая для упрощения r1≈ 0, найдем

(77.5')

Psmax =	mU2	.
	2(x1 + x'2)

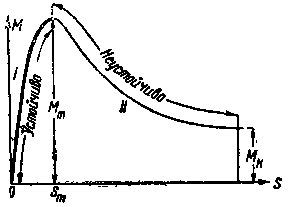Фиг. 90. Кривая зависимости крутящего момента в функции скольжения.

На фиг. 90 показана кривая зависимости крутящего момента М от скольжения s. Ясно, что чем больше х1 и х2, тем меньше получается Мmax.

Таким образом мы видим, что двигатели с большим магнитным рассеянием в пазах ротора не только будут работать с низким cos φ и что такие двигатели, кроме того, будут иметь малую величину предельного момента вращения Мmax.

Поэтому при проектировании новых двигателей обычно придают такую форму пазам ротора, при которой, с одной стороны, получается не особенно высокая величина реактанца х2 и, с другой стороны, величина магнитного сопротивления для силового потока в воздушном промежутке получается не особенно высокой 1. Для удовлетворения этих двух противоречащих друг другу требований в роторе асинхронных двигателей применяют обычно полузакрытые пазы.

1 Во избежание чрезмерного возрастания тока холостого хода I0.

Оглавление

[an error occurred while processing this directive]