ГЛАВА VII
ЯВЛЕНИЯ, ПРОИСХОДЯЩИЕ ВО ВРАЩАЮЩЕМСЯ ДВИГАТЕЛЕ
§ 58. Диаграмма ампервитков и токов вращающегося двигателя.
Предположим, что статорная обмотка асинхронного двигателя приключена к сети трехфазного тока (фиг. 71).
Тогда под влиянием токов, текущих в обмотках двигателя, появится вращающийся магнитный поток Ф, который послужит причиной появления в роторе тока I2. Последний, взаимодействуя с потоком Ф, приведет ротор во вращение, направленное в сторону вращения вращающегося потока.
Предположим, что кривая распределения м. д. с. статора (или кривая распределения ампервитков AW1) по окружности статора близ воздушного зазора имеет характер синусоиды 1 (фиг. 80).
1 В действительности кривые м. д. с. имеют "ступенчатый" характер и всегда отличаются несколько по форме от синусоиды. Разница, однако, по форме между действительными кривыми и синусоидой не особенно велика, так что при изучении работы асинхронных двигателей часто можно приближенно принимать синусоидальное распределение магнитной индукции в воздушном зазоре.
Если нам известно число пар полюсов р асинхронного двигателя и число периодов питающего тока f1, то число оборотов в минуту кривой AW1 будет
| n1 = | 60f1 |
| p |
На фиг. 80 кривая распределения ампервитков статора показана в виде синусоиды с амплитудой AW1.
| Фиг. 80. Ампервитки статора и ротора и их результирующие. | 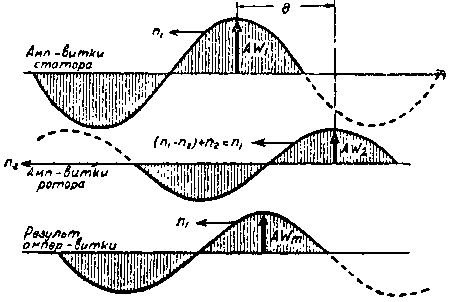 |
Теперь обратимся к ротору синхронного двигателя. Предположим, что ротор будет делать в минуту число оборотов п2 (немного меньше, чем синхронное число оборотов n1), и, следовательно, наш ротор будет отставать ("скользить") относительно вращающегося потока Ф.
Число оборотов скольжения в 1 мин. будет равно разности n1— n2.
Под влиянием тех токов, которые текут во всех трех фазах ротора, последний создаст, так же как и статор, некоторую м. д. с.
Можно принять в первом приближении, что кривая распределения ампервитков ротора вдоль его окружности будет, так же как и для статора, синусоидальной; эта кривая с амплитудой AW2 показана на фиг. 80.
Найдем скорость перемещения кривой AW2 относительно проводов обмотки ротора.
Выше было сказано, что вращающееся поле пересекает стержни роторной обмотки с разностью скоростей
n1— n = ns,
ns = s • n1,
М. д. с. AW2, создаваемая потоками роторной обмотки, "скользит" относительно проводов роторной обмотки, как было сказано, со скоростью, пропорциональной скольжению,
ns = s • n1.
Так как сама обмотка ротора перемещается в пространстве со скоростью n2, то кривая м. д. с. ротора должна перемещаться в пространстве со скоростью, соответствующей сумме: n2 + ns.
На основании (58,1) и (58,1а) найдем
п2 + ns = n2 + (п1 — п2) = п1.
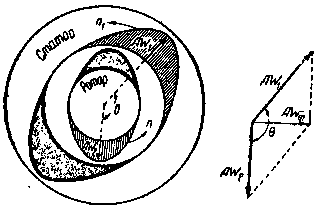 |
| Фиг. 81. Пространственная диаграмма ампервитков статора и ротора. |
Последнее выражение показывает, что кривая ампервитков ротора AW2 движется в пространстве с такой же скоростью, как и кривая ампервитков AW1 статора, независимо от того, вращается ли ротор или нет. Это свойство кривой AW2, как будет видно ниже, дает возможность построить векторную диаграмму ампервитков для вращающегося двигателя. На фиг. 81 показаны кривые распределения ампервитков в статоре AW1 и роторе AW2 для некоторого момента времени, причем для наглядности всюду кривая м. д. с., соответствующая северному полюсу, показана линейчатой штриховкой, а кривая, соответствующая южному полюсу, показана темной.
Мы видим из фиг. 81, что векторы AW1 и AW2 образуют между собой угол, равный в.
Ампервитки AW1 и AW2 могут быть сложены по правилу параллелограмма. В результате сложения у нас получатся равнодействующие ампервитки AW0, которые и служат причиной появления вращающегося потока Ф.
Здесь следует еще раз подчеркнуть то обстоятельство, что частота токов I1, создающих ампервитки статора AW1, и частота токов ротора I2, создающих ампервитки AW2, неодинакова.
Таким образом на первый взгляд может показаться, что векторы AW1 и AW2, изображающие собой на фиг. 81 (справа) ампервитки, создаваемые токами разных частот, не могут быть геометрически друг с другом сложены.
Однако при этом мы должны иметь перед глазами левый чертеж фиг. 81, из которого видно, что кривая AW2 в пространстве движется с такой же скоростью, как и кривая AW1, т. е. векторы AW1 и AW2 на фиг. 81 должны вращаться в пространстве с одинаковой скоростью, что дает нам право их геометрически складывать.
Таким образом мы видим, что диаграммы ампервитков и токов фиг. 73 (которые были нами построены для неподвижного двигателя) имеют совершенно такой же вид и для двигателя вращающегося.
