ГЛАВА XI
ПОТЕРИ и К. П. Д.
§ 109. Экспериментальное исследование явления "вытеснения тока"1 (опыты К. И. Шенфера и А. И. Москвитина).
Как известно, переменный ток распределяется неравномерно по сечению провода, находящегося в пазу электрической машины.
Это явление, которому присвоено название "вытеснение тока", имеет большое практическое значение как вредное, вызывающее нерациональное использование меди во всех электрических машинах переменного тока, и как полезное в применении к безреостатному пуску в ход асинхронных моторов. Вместе с тем явление это представляет весьма большой теоретический интерес, и аналитическому исследованию его посвящено много работ.
Общий закон изменения силы и фазы тока по высоте проводника был дан Фильдом (Field, "AIEE", 1905).
Дальнейшее исследование и применение к разнообразным случаям производили Эмде ("Е. и. М.", 1908, 1922), Роговский ("Arch. f. El.", В. 2), Рихтер ("Arch. f. El.", В. 3) и ряд других авторов.
1 См. "Вестник теоретической и экспериментальной электротехники", 1928, № 10. К. И. Шенфер и А. И. Москвитин, Экспериментальное исследование явления вытеснения тока.
Выше в кратких чертах была пояснена сущность этого явления.
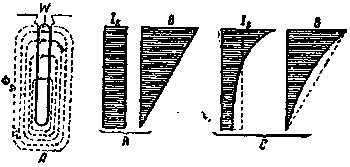
На фиг. 117, А, показан медный провод W, заложенный в узкий и глубокий паз. Если бы по проводу W протекал постоянный ток, то плотность тока в проводе во всех точках его сечения была бы одинакова.
На фиг. 117, В, показана кривая распределения плотности тока Is для этого случая; как видно из этой фигуры, эта кривая имеет вид прямоугольника.
На фиг. 117, В, справа показана кривая В изменения магнитной индукции внутри паза по его высоте.
Как показано на фиг. 117, В, изменение магнитной индукции по высоте паза происходит при этих условиях по закону прямой линии.
В том случае, если по проводнику W течет не постоянный, а переменный ток, кривые Is и В получают другие очертания.
Если по проводу W будет протекать переменный ток I, то магнитный поток рассеяния Фs будет также переменным; колебания этого магнитного потока, пронизывающего провод W, будут в этом случае наводить в массиве медного провода токи Фуко I3 (фиг. 116).
 |
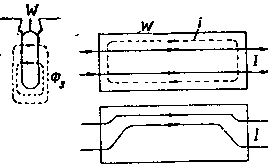 |
| Фиг. 117. А — поток рассеяния Фs; В — кривые распределения магнитной индукции В; Is— кривые распределения плотности тока. | Фиг. 118. Влияние потока рассеяния на токораспределение в проводнике. |
Эти токи Фуко I3 не совершают полезной работы и являются с этой точки зрения паразитными токами.
Токи Фуко I3 складываются с полезным током I2, в результате чего получается картина токораспределения в проводе, показанная на фиг. 116 (внизу слева). Как видно из этой фигуры, линии тока I2 при этих условиях смещаются к верхней части провода. Вследствие этого плотность тока в верхней части провода возрастает и в нижней его части убывает.
На фиг. 117, С, показана примерная кривая распределения тока в проводе для того случая, когда этот провод обтекается переменным током. Кривая распределения плотности тока и магнитной индукции В, как показывает фиг. 117, С, теряет при этом свой прямолинейный характер.
Нижеследующие формулы, выведенные из формулы Фильда 1, дают представление о количественной стороне этого явления.
Общая формула является решением диференциальных уравнений, основанных на 1-м и 2-м законах Максвелла, и представляет довольно сложное выражение. Для случая одного массивного проводника в пазу оно значительно упрощается. В этом случае мгновенное значение плотности тока is в точке сечения, находящейся на расстоянии х от нижнего края провода, дается следующей формулой:
| is = √2 | αHis0 √ch 2 αx + cos 2 αx | sin (ωt + β1— | π | + φ ), |
| √ch 2αH — cos 2αH | 4 |
1 См. также Rogowski, "Archiv f. E.", В. 2.
где
| tg β = | sh αH cos αH |
| ch αH sin αH |
| tg φ = | sh αx sin αx |
| ch αx cos αx |
Из формулы видно прежде всего, что неравномерность распределения тока по сечению тем большая, чем больше высота проводника и чем больше коэфициент:
| α = 2π | √ |
|
Ρ — удельное сопротивление проводника в Ω/cm3 (для меди Ρ = 2•10-6 Ω/cm3);
b — толщина проводника;
а — ширина паза,
т. е. вытеснение тока проявляется тем резче, чем меньше удельное сопротивление проводника и чем больше частота тока и заполнение паза. Для медных проводников при совершенном заполнении паза и частоте f = 50 Hz коэфициент α = 1.
Для тех же проводников при другой частоте f и другом заполнении паза b/a будет
| α = 1 | √ |
|
Так как в формулу входит только произведение αH, а не α и H порознь, то совершенно одинаковую картину распределения тока можно получить, изменяя как высоту H, так и коэфициент а, например, изменяя частоту.
При высоких проводниках, т. е. когда αH > 1, формула значительно упрощается, так как круговыми функциями можно пренебречь сравнительно с гиперболическими. В этом случае отношение действительной плотности тока is к плотности, вычисленной по сечению is0 = I /q, будет
| is | = √2 αH | √ch 2αx | . |
| is0 | √ch 2αH |
Для верхнего края провода (х = Н) эта формула приобретает вид, очень удобный для быстрых подсчетов:
| is | = √2 αH | . |
| is0 |
Таким образом при проводнике 4 cm высотой плотность тока в верхнем крае будет около 5,5 раз больше средней.
Из формулы (109,1) нетрудно вывести один коэфициент, которым мы вос-пользуемся для проверки опытных данных, именно коэфициент γ, равный отношению плотности тока в верхнем крае проводника, к плотности тока в нижнем крае:
| γ = | is max | . |
| is min |
Этот коэфициент характеризует интенсивность вытеснения тока.
Для верхнего края (х = Н) будет
| is max = √2 αН | √ch 2 αH + cos 2 αH | . |
| √ch 2 αH - cos 2 αH |
Для нижнего края (х = 0)
| is max = √2 αН | √2 | . |
| √ch 2 αH - cos 2 αH |
| γ = | is max | = | 1 | √ch 2 αH + cos 2 αH. |
| is min | √2 |
Экспериментальное исследование "вытеснения тока" до сих пор никем не производилось. Некоторыми авторами (см., например, Esau, "Annal. d. Physik", 1908) измерялось лишь эффективное сопротивление проводника, заложенного в паз, при переменном токе.
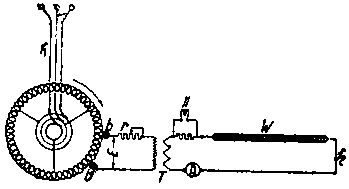 |
| Фиг. 119. Расположение опыта. |
Автор настоящей книги и инж. А. И. Москвитин задались целью выяснить опытным путем кривые распределения плотности тока и магнитной индукции для провода, заложенного в паз.
На фиг. 119 показана схема, применявшаяся при опыте. В качестве источника э. д. с. переменного тока, частоту которой можно изменять в широких пределах, был использован ротор трехфазного коллекторного двигателя Шрагэ. Если подвести из сети L трехфазный ток частоты f1 к трем контактным кольцам на фиг. 119, обмотка ротора создаст вращающееся поле Ф.
Если привести при этом во вращение ротор в обратную сторону по сравнению с вращением потока Ф, мы можем получить между щетками b— b на коллекторе э. д. с. Е разной частоты. При неподвижном роторе э. д. с. Е будет иметь частоту сети f2 = f1, при вращении ротора в сторону, обратную вращающемуся потоку, частота э. д. с. Е будет меньше частоты сети и будет убывать по мере возрастания скорости ротора; при синхронной скорости ротора частота f2 = 0, т. е. между щетками b — b в этом случае мы будем иметь напряжение Е постоянного тока.
При вращении ротора по направлению поля частота э. д. с. Е будет больше частоты сети и при скорости, равной синхронной, будет f2 = 2f1, т. е. 100 Hz.
Таким образом ротор двигателя Шрагэ позволяет с большим удобством изменять частоту э. д. с. Е между щетками b— b.
Требуемый ток (порядка 400 А) получался при посредстве трансформатора (фиг. 119) с большим передаточным числом, первичная обмотка которого последовательно с регулирующим реостатом r была приключена к щеткам b— b. Вторичная обмотка, состоявшая из нескольких витков толстого кабеля, была замкнута на испытуемый провод W, заложенный в паз.
В цепь провода W были включены для измерения тока амперметр А и шлейфа осциллографа II, позволяющая записать форму кривой переменного тока, текущего в испытуемом проводе W (в данном случае ток был чисто синусоидальный).
На фиг. 120 показан провод W, питаемый переменным током, как было описано выше (фиг. 119). Как видно из фиг. 120, провод W заложен в паз. Для измерения величины магнитной индукции в пазу на различной высоте в паз была заложена узкая и длинная катушка из тонкой медной проволоки а (на чертеже схематически изображена в виде одного витка).
Когда катушка а присоединена к шлейфу осциллографа I, пульсации магнитного потока рассеяния будут вызывать в катушке а переменный ток i, величина которого (при данной частоте f) может быть принята пропорциональной той магнитной индукции, которая наблюдается внутри паза в том месте, где расположена в данный момент катушка а.
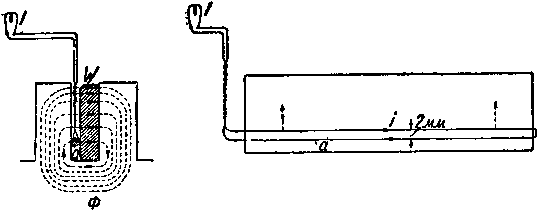 |
| Фиг. 120. Опыт, выясняющий кривую распределения магнитной индукции паза. |
Располагая катушку а на различных расстояниях от основания паза и измеряя при помощи шлейфа осциллографа I соответственную э. д. c., индуктированную пульсациями потока рассеяния в этой катушке, мы можем в различных местах паза найти величину магнитной индукции потока рассеяния.
 |
| Фиг. 121. Приспособление для перемещения измерительной шпули в пазу. |
На фиг. 121 эта катушка а, наклеенная на картонный лист, схематически изображена в виде одного витка. Посредством штанги 4 и реечной передачи 5 она сцеплена с валом барабана осциллографа 6. Таким образом медленному вращению барабана осциллографа будет соответствовать медленное передвижение катушки по высоте паза, и шлейф, приключенный к ней, запишет кривую, приблизительный вид которой изображен на фиг. 122, А. На этой фигуре изображена (слева) синусоида с постепенно увеличивающимися ординатами. Частота этой синусоиды равна частоте тока, питающего провод W. Ординаты этой синусоиды пропорциональны соответственным значениям магнитной индукции потока рассеяния внутри паза.
Как видно из этой фигуры, величина магнитной индукции потока рассеяния возрастает по мере приближения витка а к верхней части паза.
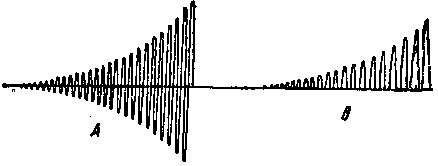 |
| Фиг. 122. Кривые распределения плотности тока. |
Если прикрыть светонепроницаемой бумагой нижнюю часть фотографической пленки, на которой происходит запись осциллогрaфической кривой, то получится кривая, изображенная на фиг. 122, В. Таким образом верхняя огибающая осциллограммы фиг. 122, В дает нам в некотором масштабе кривую распределения магнитной индукции потока рассеяния внутри паза по его высоте 1. Кривые распределения плотности тока внутри массивного проводника по его высоте были получены методом, в основе которого лежат следующие соображения.
1 Настоящий метод применяется впервые. Он может быть назван методом "пространственной" осциллографической съемки, так как получающиеся диаграммы характеризуют изменение электромагнитной величины не по времени (как обычно), а по пространству (по высоте паза).
1. При не слишком малом отношении высоты проводника к его толщине b и при нормальных размерах паза (ширина не больше 2 cm) плотность тока одинакова для всех точек сечения, лежащих на одной высоте. Таким образом, чтобы знать распределение плотности тока внутри проводника, достаточно изучить распределение ее по поверхности.
2. На некотором расстоянии от торцевых концов внутри паза линии тока идут параллельно длине массивного проводника.
3. Линии потока рассеяния в пазу идут перпендикулярно стенкам.
На основании этих соображений для выяснения распределения плотности тока внутри провода W по его высоте применялась схема, изображенная на фиг. 123. На этой фигуре означают:
G — источник э. д. с. переменного тока (типа Шрагэ, фиг. 119);W — медный проводник, заложенный в паз и питаемый переменным током I:
1 — 2 — два медных пружинящих острия, соединенные при помощи проводов со шлейфой осциллографа I (провода 1 — 2 прикреплены к жесткому картонному листу К).
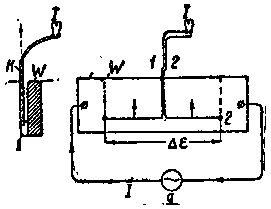 |
| Фиг. 123. Опыт, выясняющий кривую распределения плотности тока в сечении провода |
Перемещая картонный лист К с медными остриями 1— 2 снизу вверх, как показано на фиг. 123 (слева), мы можем измерить при помощи скользящих контактов 1— 2 омическое падение напряжения ΔЕ = ir между точками 1— 2, пропорциональное плотности тока в данном волокне провода.
Для того чтобы в витке, образованном проводниками 1— 2 и соответственным волокном медного провода W, не наводилась дополнительная э. д. с. вследствие пульсации потока рассеяния, соединительные проводники 1— 2 должны быть протянуты по прямой линии параллельно длине провода и затем перевиты бифилярно, как показано на фиг. 123 (справа).
Связав картон К и острия 1 — 2, скользящие по боковой поверхности провода W, с валом барабана осциллографа (таким же образом, как на фиг. 121), мы можем при помощи шлейфы осциллографа I записать кривую изменения плотности тока по высоте массивного провода W.
На фиг. 124—126 изображены осциллограммы, полученные при опыте.
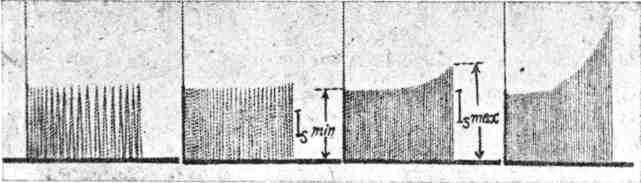
На фиг. 124 приведены осциллограммы, характеризующие распределение плотности тока внутри медного провода по высоте паза при разных частотах (f2 = 12,5, f2 = 25, f2 = 50, f2 = 100 Hz); при этом размеры провода были 5 х 28 mm и размеры паза 9 х 30 mm.
Как видно из фиг. 124, при малой частоте, f = 12,5 Hz, мы имеем почти равномерное распределение плотности тока в проводе; по мере возрастания частоты тока, текущего в проводе, неравномерность распределения плотности тока выражается все резче и резче.
Так, при частоте f2 = 50 Hz отношение крайних ординат осциллограммы, Дающих в некотором масштабе плотность тока в крайнем верхнем волокне (is max) и в нижнем волокне — у основания паза (is min), получается
| γ = | is max | = 3,8. |
| is min |
При f2 = 100 Hz согласно фиг. 124 это отношение будет уже значительно больше:
γ = 9.
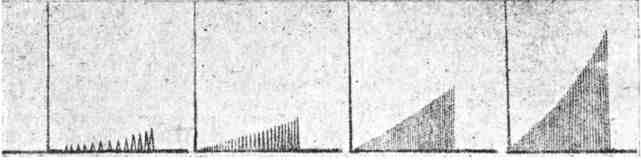
При проводе меньшей толщины (2 х 28 mm) и несколько большего удельного сопротивления, заложенном в паз того же размера, что и в предыдущем случае (9 х 30 mm), получились осциллограммы, изображенные на фиг. 125.
Как видно из сравнения фиг. 124 и 125, степень неравномерности распределения плотности тока, характеризующаяся отношением, для провода согласно фиг. 125 получается меньше, чем в предыдущем случае.
 |
| Фиг. 124. Кривые распределения плотности тока Is по высоте при-вода при разных частотах (f = 12,5; 25, 50, 100 Hz). Размеры провода 5x28 mm. |
 |
| Фиг. 125. Те же кривые, что на фиг. 124, но только для провода 2x28 mm. |
 |
| Фиг. 126. Кривые распределения магнитной индукции в пазах при разных частотах (f = 12,5; 25, 50, 100 Hz). |
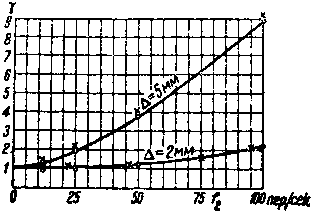 |
| Фиг. 127. Отношение плотности тока в крайнем верхнем волокне к плотности тока в крайнем нижнем волокне при разных частотах. |
По нахождении величин у для разных частот согласно фиг. 124 и 125 были построены кривые фиг. 127, из которых видно, как возрастает коэфициент неравномерности с увеличением частоты тока, питающего провод; понятно, что кривые фиг. 127 имеют частное значение для проводов и пазов данных размеров.
Рядом с экспериментальными точками знаками х помечены точки, вычисленные для данного случая по формуле (109,1). Как видно, экспериментальные точки достаточно близки к теоретическим.
На фиг. 126 приведены осциллограммы, характеризующие распределение индукции магнитного рассеяния по высоте паза для проводника размером 2 х 28 mm (фиг. 124); из фиг. 126 видно, что при малых частотах кривая изменения магнитной индукции рассеяние паза имеет характер прямой линии (ср. фиг. 117, В); по мере увеличения частоты мы наблюдаем некоторое искривление этой линии (ср. правую осциллограмму фиг. 126 и фиг. 117, С).
Таким образом результаты экспериментального исследования показывают правильность теоретических соображений о сущности явления "вытеснения тока".
