§ 31. Влияние характера размещения обмотки в пазах на величину обмоточного коэфициента "распределения".

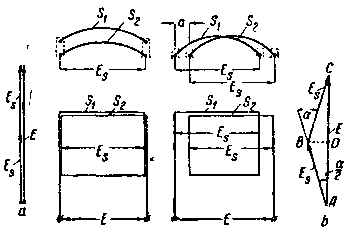Фиг. 59. Определение обмоточного коэфициента для двух витков: а) для случая совпадения осей секции (левый чертеж); б) при смещении на угол α друг относительно друга (правый чертеж).

Предположим сначала, что у нас имеется два витка — S1 и S2, расположенные в общих пазах один над другим (фиг. 59, а). Обозначим э. д. с, наведенную в каждом из этих витков (или секций), через Es ; результирующая э. д. с, наведенная в обмотке, состоящей из двух витков, будет равна сумме

E = Es+ Es = 2Es .

Предположим теперь, что секции S1 и S2 расположены в смежных пазах (фиг. 60, b). В этом случае э. д. с, наведенные в секциях S1 и S2, совпадать по фазе уже не будут и будут смещены на некоторый угол α; в случае двухполюсной схемы этот угол α будет равен по числовой величине угловому смещению между двумя смежными пазами, как показано на фиг. 59, b.

При расположении проводников, показанном на фиг. 59, b, результирующая э. д. с. Е будет меньше алгебраической суммы э. д. с. каждой секции ввиду того, что эти э. д. с, как уже было сказано, смещены теперь по фазе друг относительно друга на ∕_—) α. Складывая геометрически э. д. с. Es, мы можем найти результирующую э. д. с. E, как показано на фиг. 59, b.

Из получившегося треугольника ABC (фиг. 59, b) мы можем найти, что

AD = АВ• cos	α	;
	2

или

1	•Е = Еs•cos	α
2	•Е = Еs•cos	2

откуда

Е = 2Еs•cos	α
	2

Обмоточный коэфициент "распределения" для этого случая будет равен

(31.1)

kp =	E	=	2Escos(α/2)	= cos	α	;
	∑Es		2Es		2

Полученная формула (31,1) показывает, что обмоточный коэфициент зависит от угла α, или, другими словами, зависит от характера расположения обмотки в пазах.

Оглавление

Вперед

[an error occurred while processing this directive]

АСИНХРОННЫЕ МАШИНЫ

ГЛАВА III ОБМОТОЧНЫЙ КОЭФИЦИЕНТ

§ 31. Влияние характера размещения обмотки в пазах на величину обмоточного коэфициента "распределения".

АСИНХРОННЫЕ
МАШИНЫ

ГЛАВА III
ОБМОТОЧНЫЙ КОЭФИЦИЕНТ