АСИНХРОННЫЕ
МАШИНЫ

ВВЕДЕНИЕ

§ 5. Вращающееся магнитное поле, создаваемое трехфазным током.

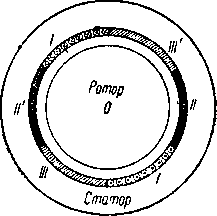
На практике при передаче электрической энергии, как известно, главным образом, применяется трехфазный ток. Поэтому рассмотрим расположение (фиг. 12), дающее возможность получения вращающегося потока при трехфазной системе.

На этой фигуре в разрезе изображены три катушки I — I', II—II' и III — III', обтекаемые трехфазным током, причем для наглядности пояса токов, принадлежащих разным фазам, изображены разной штриховкой. Как видно из фиг. 12, оси этих трех катушек относительно друг друга в пространстве составляют угол в 120°.

Обозначим мгновенные значения токов, текущих в катушках в какой-нибудь момент времени, через i1 , i2 и i3 .

Каждая из трех изображенных на фиг.12 катушек в отдельности создает магнитный поток, пульсирующий с частотой сети. Предположим для упрощения задачи, что кривая распределения магнитной индукции в воздушном зазоре вдоль окружности ротора, создаваемая каждой фазной обмоткой статора в отдельности, представляет собой синусоиду. Таким образом при наличии трех обмоток в статоре I—I', II—II' и III — III' мы будем иметь дело с тремя соответственными кривыми магнитной индукции с синусоидальным распределением, смещенными друг относительно друга по окружности ротора на 120°.

Фиг. 12. Расположение обмотки статора трех-фазного асинхронного двигателя

Амплитуды этих трех синусоид не будут постоянными, но будут изменяться в соответствии с изменением токов, текущих в трех фазах обмотки статора. Если, например, в фазе I ток будет иметь значение

то амплитуда кривой распределения магнитной индукции в воздушном зазоре будет равна

В тот момент, когда ток в фазе I будет равен максимальному значению, амплитуда кривой магнитной индукции достигнет также своего максимального значения:

Для какого-нибудь момента времени t значения токов, текущих в фазах I — II — III, и соответственных амплитуд магнитной индукции даются следующей таблицей.

ТАБЛИЦА   1

Фаза	Ток	Амплитуда  магнитной индукции
I	i1 = Im • sin ωt	B1 = Вт • sin ωt
II	i2 = Im •sin (ωt— 120°)	B2 = Bm • sin (ωt — 120°)
III	i3 = Im • sin (ωt - 240°)	B3 = Вm • sin (ωt - 240°)

Фиг. 13. Катушки I, II и III, сидящие на общем керне

Нашей задачей является нахождение магнитной индукции В123 , получающейся в результате одновременного существования всех трех синусоид   с амплитудами В1, В2 и В3 .

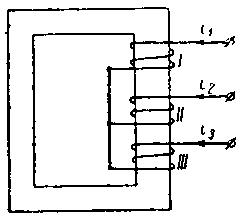
Для получения этой результирующей индукции В123 было бы неправильно складывать значения В1, В2 и В3 алгебраически. Это можно было бы сделать только в том случае, если бы оси всех катушек I, II и III совпадали, т. е. если бы мы имели расположение, характеризуемое фиг.13, на которой изображены 3 катушки I — II — III, сидящие на общем керне и соединенные между собой в звезду.

В этом случае мы имели бы для результирующей магнитной индукции следующее значение:

или

Выражение, стоящее в прямых скобках последнего уравнения, как это нетрудно доказать, оказывается равным нулю; таким образом при этих условиях мы получаем В123 = 0; следовательно, мы видим, что при условиях фиг.13 результирующий поток будет равен нулю. При условиях же фиг.12 оси катушек I, II и III не совпадают друг с другом, но составляют друг с другом угол 120°. Таким образом для нахождения результирующей величины В123 магнитные индукции этих катушек В1 , В2 и В3 должны быть сложены не алгебраически, но геометрически.

Поэтому для нахождения результирующей величины В123 найдем сумму проекций величин В1, В2 и В3 на какую-нибудь ось, например, ось катушки I

На основании данных таблицы последнее уравнение примет следующий вид:

Вынося постоянную величину В за скобки и производя простые тригонометрические преобразования, найдем окончательно

B123 =	3	Вm • sin ωt.
	2

Это уравнение показывает, что при трехфазной системе обмоток согласно фиг. 12 результирующий вектор получается

B123 = 3 Вm. 2

причем В123 вращается в пространстве с постоянной угловой скоростью ω.

Такой результат получается, однако, лишь в том случае, если кривые распределения м. д. с, создаваемые обмотками I, II, III вдоль окружности статора или ротора, являются синусоидами и если токи, питающие эти обмотки, будут строго синусоидальны. В действительности же по большей части кривые м. д. с. и токи, питающие обмотки I, II, III, имеют высшие гармонические составляющие, вследствие чего, как можно показать, в результирующем магнитном поле должны также появиться высшие гармоники.