ГЛАВА XXX
НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ, ПРОИСХОДЯЩИЕ В АСИНХРОННОМ ДВИГАТЕЛЕ ПРИ ПЕРЕХОДНЫХ РЕЖИМАХ
§ 263. Внезапное включение на сеть асинхронного двигателя при разомкнутом роторе.
Как известно 2, в момент приключения к сети переменного тока какой-либо катушки с самоиндукцией L и с активным сопротивлением r мы можем получить кривую изменения тока разной формы в зависимости от того, в какой момент времени произошло приключение к сети.
Статор асинхронного двигателя с разомкнутым ротором является своего рода катушкой самоиндукции L, как это показано для случая однофазной цепи на фиг. 308,
Как известно, для контура фиг. 308, можно написать уравнение 2
2 См. акад. В. Ф. Миткевич, Физические основы электротехники.
| u = ir + L | di | . |
| dt |
Для синусоидального напряжения u = Um sin ωt решение этого диференциального уравнения приводит к следующему хорошо известному результату:
| i = | Um | sin (ωt — φ).. |
| √r2 + ω2L2 |
Это решение дает уравнение принужденных колебаний (с частотой сети).
Однако уравнение (261,2) дает еще другое решение, которое приводит к так называемым свободным колебаниям или выравнивающему току, который длится до тех пор, пока длится переходный режим.
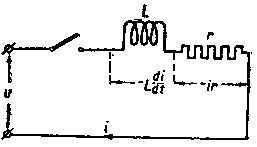 |
Фиг. 308. Контур с катушкой |
Этот переходный процесс совершается под влиянием констант контура L и r и совершенно не зависит от приложенного напряжения. Таким образом "свободный", или "выравнивающий", ток может быть получен, если в уравнении (262,1) напряжение на зажимах положить равным нулю (т. е. u = 0), замкнув на короткое самые зажимы. В этом случае мы получим уравнение
| ir + L | di | = 0, |
| dt |
решение которого дает величину свободного тока icв :
| icв = Ae |
|
Таким образом полное решение 1 диференциального уравнения будет
1 См. проф. К. А. Круг, Основы электротехники, стр. 794.
| i = | Um | sin (ωt — φ)+ Ae |
|
|||||||
| √r2 + ω2L2 |
| i = | Um | [sin (ωt — φ)— sin (α — φ) e |
|
] | |||||||
| √r2 + ω2L2 |
i = inp + icв,
где inp — ток принужденного режима и icв —свободный ток.
Таким образом свободный ток имеет величину
| i = | Um | sin (α— φ)e |
|
|||||||
| √r2 + ω2L2 |
По своей величине свободный ток icв устанавливается таким, что он всегда противоположен и равен тому току принужденных колебаний inp, который должен был бы установиться в начальный момент времени, если бы не было переходного процесса.
На фиг. 308а показаны в виде примера кривые тока принужденного режима inp и свободного тока icв. Из фиг. 308а видно, что свободный ток icв по существу является постоянным затухающим током.
Из чертежа ясно, что наибольший бросок тока im получится для
того случая, когда включение произойдет в момент α - φ = π/2.Если затухание свободного тока ice при этом будет невелико, то бросок тока получит максимально возможное значение
im ≈ 2Inp .
Заметим, что все эти рассуждения справедливы для того случая, когда дроссель L совершенно не насыщен.
В противоположном случае, как будет видно ниже, бросок тока может быть значительно больше двойного Inp.
Если случайно включение произойдет в тот момент, когда α - φ = 0, то можно показать, что "свободный" ток будет равен нулю.
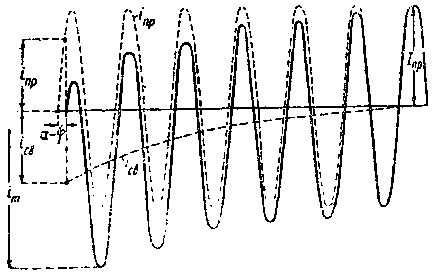 |
| Фиг. 308а. |
Из сказанного ясно, что свободный ток icв имеет очень большое значение в переходных процессах.
Таким образом этот свободный ток в переходных процессах играет такую роль, что он переводит двигатель из одного состояния нагрузки в другое, т. е. из состояния начального режима (включение на сеть) к установившемуся режиму (нормальная работа).
Перейдем теперь от теоретического к действительному случаю и рассмотрим процессы включения на сеть статора асинхронного двигателя (фиг. 308).
Рассматривая процессы, происходящие в статорной обмотке S, в момент включения статорной. обмотки на сеть (при разомкнутом роторе R), мы получим такие же кривые включения, как было показано на фиг. 308а.
