АСИНХРОННЫЕ
МАШИНЫ

ГЛАВА III
ОБМОТОЧНЫЙ КОЭФИЦИЕНТ

§ 29. Понятие об обмоточном коэфициенте.

Представим себе синхронный трехфазный генератор, в статоре которого расположена кольцевая обмотка, соединенная в треугольник согласно фиг. 56.

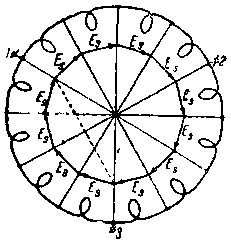Фиг. 56. Векторная диаграмма э.д.с. Es, индуктируемых в секциях обмотки статора синхронного генератора.

Предположим далее, что внутри такого статора вращается двухполюсный электромагнит возбуждения, создающий в воздушном зазоре магнитную индукцию с синусоидальным распределением вдоль окружности и выполненный в виде ротора с обмоткой, обтекаемой постоянным током, наподобие тех конструкций, которые являются обычными для турбогенераторов (этот ротор на фиг. 56 не показан).

Если такой двухполюсный ротор будет вращаться с постоянной скоростью, то в каждой из секций кольцевой обмотки фиг. 56 будет наводиться э. д. с. Es. При этом эффективное значение величины этой э. д. с. Es будет для всех секций одинаково, но по фазе э. д. с. Es будут друг от друга отличаться.

Такое же явление сдвига фаз между э. д. с. Es , индуктированными в отдельных секциях, мы имеем в статоре асинхронного двигателя; эти э. д. с. Es в асинхронном двигателе вызываются вращающимся магнитным потоком. Сдвиг фаз между э. д. с. Es обусловлен различным расположением по окружности статора отдельных секций обмотки.

Если сложить между собой геометрически э. д. с. Es , то получится замкнутый правильный многоугольник, как показано на фиг. 57.

При увеличении числа секций статорной обмотки число сторон правильного   многоугольника,    образованного    векторами    Es ,    возрастает, и в пределе многоугольник   векторов   превращается   в   окружность.

Электродвижущую силу,   индуктированную в каждой   секции, можно найти из формулы

где f — число периодов в секунду;

ws—число витков одной секции;

Ф — магнитный поток, сцепленный с рассматриваемой секцией.

Обозначив через N   число   секций,   заключенное   в обмотке каждой фазы, выразим число витков одной фазы через

Найдем теперь э. д. с. E1, индуктированную в одной фазе обмотки. На первый взгляд может показаться, что должно быть

Однако выражение (29,2) по отношению к данным фиг. 56 неверно.

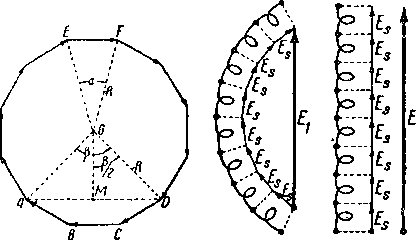Фиг. 57—58. Сложение э. д. с. для случая совпадающих осей витков (правый чертеж) и случаи витков, расположенных по окружности статора (левый чертеж).

Это равенство (29,2) было бы справедливо только в том случае, если бы э. д. с. Es, индуктированные в каждой из секций, совпадали по фазе; последнее имеет место, например, в обмотке трансформаторов, в которых, как известно, по большей части оси всех витков или секций отдельной фазы совпадают друг с другом (фиг. 58, правый чертеж).

В статоре асинхронного двигателя или синхронной машины отдельные секции обмотки смещены в пространстве друг относительно друга (фиг. 58 левый чертеж); поэтому результирующая э.д.с. Е1, индуктированная в одной фазе, будет меньше алгебраической суммы всех э. д. с. Es , наведенных   в секциях, т. е. мы будем иметь

или

Для того чтобы последнее выражение (29,3) превратить в равенство, необходимо ввести в расчет некоторый поправочный множитель kр , меньший единицы; в этом случае мы получим;

Из последнего выражения можно найти

Поправочный множитель kр, входящий в выражение (29,4), обычно носит название обмоточного коэфициента.

Как показывает формула (29,5), обмоточный коэфициент kр по числовой величине равен отношению геометрической суммы э. д. с, наведенных в отдельных секциях, к их алгебраической сумме.

Этот обмоточный коэфициент будем в дальнейшем называть обмоточным коэфициентом распределения и обозначим его kр . Величина коэфициеита kр зависит от характера распределения обмотки в пазах, т. е. зависит от числа пазов на полюс и фазу q.

Влияние укорочения шага обмотки. В том случае, если шаг обмотки (двухслойной "американской" или катушечной "равносекционной") меньше полюсного деления, т. е. если у<τ, это влечет за собой уменьшение индуктированной э. д. с. в каждом витке, что можно учесть помножением всего числа витков на коэфициент, меньший единицы: kу .

Величина этого обмоточного коэфициента "укорочения" может быть найдена из уравнения:

ky = cos(	π		τ - y	).
	2		τ

При у = τ, т. е. при "неукороченной" обмотке из этой формулы получаем

Если же, например, мы имеем обмотку с укороченным шагом у = 4/5 τ, коэфициент укорочения будет равен:

ky = cos(	π		τ - 4/5 τ	);
	2		τ

ky = cos(	π	•	1	) = 0.951.
	2		5

При укорочении у = 6/7, получится

Как было выяснено выше, надлежащим укорочением шага обмотки можно добиться полного уничтожения какой-либо одной наперед заданной высшей гармоники в кривой э. д. с. 1.

Например, для уничтожения пятой гармоники следует принять шаг обмотки у = 4/5 τ, т. е. укоротить его на одну пятую.

Если же мы желаем уничтожить седьмую гармонику, то шаг следует укоротить на одну седьмую, т. е. взять его равным: у = 6/7 τ.

Полная, результирующая величина обмоточного коэфициента определится как произведение коэфициента распределения и коэфициента укорочения:

В случае катушечных обмоток с неравными секциями, согласно фиг. 16, имеем k1 = kp. При катушечной равносекционной обмотке следует учитывать оба обмоточных коэфициента kp и kу.

---

1 См. § 15.

---

Для краткости величину результирующего обмоточного коэфициента ниже будем обозначать через k1 (для статора) и через k2 (для ротора).