ГЛАВА XXV
КАСКАДНОЕ СОЕДИНЕНИЕ ДВУХ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
§ 228. Явления, происходящие при каскадном соединении асинхронных двигателей с однофазным ротором.
До сих пор вышеописанное явление Гергеса было известно только в двигателях, работающих в одиночку. Чрезвычайно интересно также исследовать вопрос, как будут вести себя асинхронные двигатели в каскадном соединении в том случае, когда ротор одного из них однофазный.
 |
| Фиг. 228. Кривые моментов вращения. |
Насколько известно автору этой книги, этот вопрос до сих пор еще никем затронут не был, поэтому в настоящей главе сделана попытка исследовать каскадное соединение с этой точки зрения 1.
1 Проф. К. И. Шенфер, Каскадное соединение двух асинхронных двигателей с однофазным ротором. Труды Государственного эксперимент, электротехнического института № 5, 1924. Prof. Claudias Schenfer, Die Kaskadenschaltung; zweier Asynchronmotoren, von denen einer einen Einphasenrotor bezitzt, "Elektr. Zeitschr." № 22, 1925, и "Elektr. und Masch", № 27, 1925.
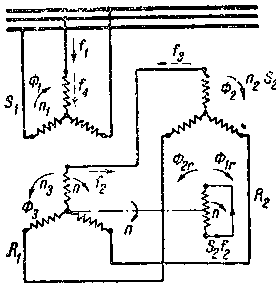
На фиг. 263 и 264 схематически изображено такое каскадное соединение двух асинхронных двигателей.
На этой фигуре означают:
L — трехфазную линию;
S1— статор первого двигателя;
R1 — ротор первого двигателя;
S2 — статор второго двигателя;
R2 — ротор второго двигателя.
Как видно из этой фигуры, ротор первого двигателя соединен со статором второго двигателя, и оба ротора агрегата сидят на одном общем валу.
Если замкнуть на короткое только одну фазу ротора R2 второго двигателя, как показано на фиг. 263, то можно ожидать по аналогии с явлением Гергеса в одном двигателе, что каскадный агрегат также приобретает способность работать устойчиво с несколькими новыми скоростями.
Постараемся найти эти скорости. Обозначим:
р1 — число пар полюсов первого статора;
р2— число пар полюсов второго „
f1 — число периодов тока сети;
s1 — скольжение ротора первого двигателя;
s2 — скольжение ротора второго „
п — число оборотов в минуту агрегата;
п1 — скорость вращающегося потока Ф1 относительно статорной обмотки первого двигателя, создаваемого токами частоты сети f1;
f2 — число периодов тока в роторе первого двигателя, вызываемого потоком Ф1;
п2 — скорость вращающегося потока Ф2 относительно статорной обмотки второго двигателя S2, вызванного токами частоты f2;
f3 — число периодов токов "скольжения", вызванных "инверсным полем "Ф" в статоре второго двигателя;
п3 — скорость поля Ф3 относительно обмотки ротора R1 первого двигателя, вызванного токами частоты f3;
f4 —число периодов токов "скольжения", вызванных потоком Ф3 в статоре S1 первого двигателя.
Токи периодичности сети f1, текущие в статорной обмотке S1 первого двигателя (фиг. 264), вызывают в ней вращающееся магнитное поле Ф1; число оборотов в минуту этого поля будет
| п1 = | 60 • f1 | . |
| р1 |
Если при этом агрегат будет вращаться с числом оборотов n в ту же сторону, что и поле Ф1, последнее вызовет в роторе токи периодичности f2 = s1f1; имея в виду, что s1 = 1 - n/n1, получим
| f2 = f1(l - | n | ); |
| n1 |
или на основании уравнения (228,1)
| f2 = f1- | np1 | . |
| 60 |
Токи периодичности f2 создают вращающийся поток Ф2 в статоре S2 второго двигателя; число оборотов этого потока будет
| п2 = | 60 • f2 | . |
| р2 |
Поле Ф2 вызывает в роторе R2 второго двигателя (фиг. 264) токи периодичности скольжения s2f2, где
s2 = l - n/n2.
Если ротор второго двигателя будет однофазным, как это показано на фиг. 262, то ток периодичности скольжения вызовет в нем пульсирующее однофазное поле, которое можно разложить на 2 потока, вращающихся в разные стороны с одинаковой относительно обмотки R2 скоростью: "прямое поле" Ф1r и "инверсное поле" Ф2r.
Поле Ф2r, так же как это было указано выше в § 227 для одного двигателя, вызовет в статоре S2 токи, частота которых f3 будет отличаться от частоты f2; связь между этими частотами получится из уравнения
f3 = (2s2 - l)f2.
Присоединяя сюда уравнения (228,3) и (228,4), получим
| f3 = f2-2 | np2 | . |
| 60 |
Токи частоты f3, индуктированные в статоре S2 второго двигателя, как видно из фиг. 264, будут циркулировать также и в роторе R1 первого двигателя и вызовут в нем вращающееся поле Ф3; число оборотов этого вращающегося поля относительно ротора будет
| п3 = | 60 • f3 | . |
| р1 |
Поле Ф3 будет вращаться в сторону, обратную вращению агрегата (фиг. 264), и потому будет перемещаться относительно статора S1 первого двигателя со скоростью скольжения и будет наводить в нем токи с числом периодов
| f4 = f3(l - | n | ); |
| n3 |
или на основании уравнения (228,5')
| f4 = f3- | np1 | . |
| 60 |
Отсюда мы видим, что в статоре второго двигателя, а также в статоре и роторе первого двигателя будет циркулировать токи двух разных частот. На фиг. 264 токи частот f3 и f4, вызванные инверсным полем ротора второго двигателя, показаны пунктирными стрелками. В случае трехфазных роторов эти токи частот f3 и f4 исчезают.
 |
| Фиг. 228. Кривые моментов вращения. |
Токи с частотой f3 и f4, взаимодействуя с соответственными потоками, могут образовать вращающие моменты, которые при известных условиях могут иметь положительные или отрицательные значения. Благодаря наличию этих дополнительных моментов каскадный агрегат может работать устойчиво при нескольких скоростях. Найдем эти скорости. Первая устойчивая скорость. Как было сказано выше, поле Ф3, создаваемое токами частоты f3 в роторной обмотке R1, в пространстве перемещается со скоростью, равной разности скорости агрегата n и относительной скорости вращения поля n3 = 60f3/p1; при n = n3 = 60f3/p1 поле Ф3 в пространстве делается неподвижным, и веледствие этого частота f4 = 0.
При п > п3 крутящий момент, вызванный взаимодействием поля Ф3 и токов частоты f4, текущих в статоре S1 (фиг. 264), делается отрицательным, т. е. тормозит движение агрегата. Если при этом тормозящий момент будет больше или в крайнем случае равен положительному моменту агрегата, создаваемому потоками, вращающимися в сторону вращения агрегата, то последний не будет в состоянии перейти эту критическую скорость. Таким образом условием, на основании которого может быть найдена эта критическая скорость, будет
f4 = 0,
| п = | 60 • f3 | . |
| р1 |
Преобразуя это выражение на основании уравнений (228,5) и (228,2), получим
| [(f1 - | np1 | ) - 2 | np2 | ], | |
| п = 60 | 60 | 60 | |||
| p1 | |||||
или
| п = | 60 f1 | . |
| 2(p1 + р2) |
Полученное выражение показывает, что при однофазном роторе второго двигателя агрегат стремится к синхронной скорости, которая соответствует двигателю с удвоенной суммой пар полюсов обеих машин.
Если бы ротор второго двигателя был многофазным, то, как известно, каскадный агрегат стремился бы к синхронной скорости, соответствующей сумме пар полюсов обеих машин:
| п = | 60 f1 | . |
| p1 + р2 |
Таким образом простым размыканием цепи двух фаз второго ротора и превращением его в однофазный мы получаем возможность уменьшить скорость агрегата вдвое.
Сравнение уравнений (228,8) и (228,9) между собой показывает, что каскадный агрегат с однофазным ротором второго двигателя по своим свойствам сходен с каскадным агрегатом из четырех многофазных двигателей.
Разница только та, что в этом четырехмашинном агрегате в каждой из обмоток текут токи одной только периодичности, в то время как при двух машинах и однофазном роторе в обмотках машин текут токи двух разных частот (фиг. 264).
Интересно проследить путь и превращения энергии в двухмашинном агрегате с однофазным ротором (фиг. 264). Электрическая энергия тока частоты f1, подведенная к статору S1 первого двигателя, передается ротору R1 при посредстве вращающегося потока Ф1. При этом первая машина работает частично как двигатель, частично как преобразователь числа периодов, передавая неиспользованную энергию тока частоты f2 статору S2 второго двигателя. Здесь эта энергия при посредстве вращающегося потока Ф2 передается однофазному ротору R2. В последнем электрическая энергия превращается в механическую форму только частично; неиспользованная же часть энергии при посредстве "инверсного поля" Фr передается обратно статору S2.
Из статора S2 энергия в виде тока частоты f3 подводится к ротору R1 первого двигателя и отсюда при помощи вращающегося потока Ф3 перекачивается обратно в статор S1 первого двигателя в форме тока частоты f4, который замыкается через линейные провода L и затем через обмотку генератора или трансформатора, питающего эту линию.
Таким образом мы видим, что энергия, подводимая к агрегату, сначала течет в направлении от первой машины ко второй, доходит до однофазного ротора и затем течет в обратном направлении, возвращаясь к статору первого двигателя в виде тока частоты скольжения.
Вторая устойчивая скорость. "Инверсное поле" Ф2r, вызванное однофазным ротором, как уже было сказано выше, останавливается в пространстве при скольжении s2 = 1/2; при скорости агрегата немного выше этой "инверсное поле" образует тормозящий момент, поэтому агрегат вращается устойчиво при скорости близкой к
s1 = 1/2;
1 - n/n2 = 1/2;
| п = | 60 f1 | . |
| p1 + 2р2 |
Сравнивая это выражение с уравнением (228,9), замечаем, что вторая устойчивая скорость агрегата лежит выше первой. Самостоятельно агрегат этой второй скорости, даваемой уравнением (228,10), достигнуть не может. Для того чтобы довести агрегат до этой скорости, нужно или его развернуть при помощи какого-нибудь вспомогательного двигателя или сделать на время ротор второго двигателя многофазным, замкнувши все три его фазы. При работе агрегата со скоростью, близкой к даваемой уравнением (228,10), частота f3, вызываемая "инверсным полем", делается небольшой. Наоборот, частота f4 при этих условиях в значительной мере увеличивается, так как поле Ф3 начинает в пространстве при этом перемещаться быстрее.
При этом токи возросшей частоты f4, замыкающиеся через провода линии и обмотки генератора, встречают на своем пути большее кажущееся сопротивление, вследствие чего тормозящий (генераторный) момент, вызываемый этими токами, обычно не может при этих условиях достигнуть большой величины.
Третья устойчивая скорость. Для получения этой скорости необходимо приравнять к нулю число периодов в роторе R2 второго двигателя:
s2f2 = 0,
s2 = 0,
1- n/n2 = 0,
Присоединяя сюда уравнения (228,2) и (228,3), найдем
| п = | 60 f1 | . |
| p1 + р2 |
Получилось известное выражение для синхронного числа оборотов обычного каскадного соединения (с многофазными роторами).
Агрегат с однофазным ротором может вращаться устойчиво со скоростью, близкой к даваемой уравнением (228,11), но должен быть предварительно развернут от вспомогательного двигателя или каким-либо другим способом.
Четвертая устойчивая скорость. Эта скорость может быть найдена из условия
f2 = 0,
| п = | 60 f1 | . |
| p1 |
Полученное уравнение показывает, что агрегат может также устойчиво работать при скорости, близкой к скорости вращающегося Ф1 первого двигателя. Самостоятельно дойти до этой скорости агрегат, однако, не может.
