ГЛАВА XXXVI
МАГНИТНЫЕ ПОТОКИ РАССЕЯНИЯ
§ 322. Магнитная проводимость паза λп .
На фиг. 342 изображен паз с пучком проводов, заложенных в него. Предположим сначала, что длина этого паза равна 1 cm. Попытаемся найти величину магнитной проводимости λп для этого паза.
Поток, охватывающий пучок проводов, заложенных в паз, и замыкающийся поперек паза, мы можем разложить на две части:
1) часть потока, силовые линии которого охватывают весь пучок проводов и которые замыкаются поперек паза на высоте h2 + h3 + h4 (назовем магнитную проводимость этого потока через λ''п);
2) часть потока, силовые линии которого не сцеплены со всем пучком проводов и которые замыкаются поперек паза по высоте h1 (назовем магнитную проводимость этого потока через λ'п).
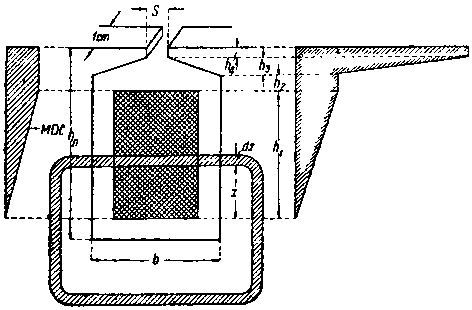 |
| Фиг. 342. Поток рассеяния в пазу. |
Представим себе силовую трубку, имеющую толщину, равную dx и проведенную на расстоянии х от нижней кромки пучка проводов (фиг. 342). Число проводов, охватываемое этой силовой трубкой, будет
| sn • | x | , |
| h1 |
Если ток в каждом проводе будет равен 1 А, то вышенаписанное выражение будет представлять собой также величину магнитодвижущей силы (измеряемой в "амперпроводах") в точке, отстоящей от нижней кромки пучка проводов на расстоянии х.
Таким образом по мере увеличения расстояния х величина м. д. с. будет возрастать, причем это возрастание будет продолжаться до тех пор, пока будет х < r; при х > r величина м. д. с. будет оставаться все время постоянной, как показано на фиг. 342 слева в виде диаграммы.
Найдем величину магнитного потока, соответствующую изображенной на фиг. 342 силовой трубке, на протяжении осевой длины паза, равной 1 cm.
Пренебрегая магнитным сопротивлением в железе, найдем приближенно величину магнитного сопротивления вышеупомянутой силовой трубки:
| Rx = | b | . |
| 0,4π • dx • 1 |
Магнитная проводимость будет равна обратной величине магнитного сопротивления
| λп = | 1 | = 0,4π | dx | ≈ 1,25 | dx | . |
| Rx | b | b |
Магнитный поток φх, соответствующий этой силовой трубке, будет равен произведению м. д. с., умноженной на магнитную проводимость; таким образом найдем
| φх = (sn | x | ) λx = 1,25 • sn • | x dx | . |
| h1 | h1 • b |
Число магнитных сцеплений для пучка проводов sn x/r , охватываемого
| Число магнитных сцеплений для пучка проводов sn | x | , охватываемого силовой трубкой, |
| r |
| (sn | x | )φх = sn | x | • 1,25 • sn | x dx | = 1,25 | x2 | • | dx | . |
| h1 | h1 | h1b | h12 | b |
Общее число магнитных сцеплений найдем, проинтегрировав вышенаписанное выражение по высоте паза в пределах от х = 0 до х = h1:
| h1 | h1 | ||||||||||||
| ∫ | 1.25 | x2 | dx | = | 1.25 | ∫ | x2dx = | 1,25 | • | h13 | = 1,25 | h1 | = λ'п. |
| h12 | b | h12b | h12b | 3 | 3b | ||||||||
| 0 | 0 |
Для тех силовых трубок, которые охватывают весь пучок проводов, заложенных в паз, пренебрегая магнитным сопротивлением пути в железе, без труда можно найти следующее выражение: 1
1 Arnold, Wechselstromtechnik, V. 1.
| λ''п = 1,25 ( | h2 | + | 2h3 | + | h4 | ). |
| b | s + b | s |
Таким образом суммарная величина магнитной проводимости будет
| λп = λ'п + λ''п = 1,25 ( | h1 | + | h2 | + | 2h3 | + | h4 | ). |
| 3b | b | s + b | s |
Для открытого паза получается
| λп = 1,25 ( | h1 | + | h2 | ). |
| 3b | b |
Для быстрых и приближенных подсчетов в случае полузакрытых пазов прямоугольного сечения можно пользоваться эмпирической формулой автора, имеющей более простой вид:
| λп ≈ 0,7 | h1 | . |
| b |
Если известны только высота паза hn и его ширина b (фиг. 342), можно пользоваться другой приближенной эмпирической формулой автора
| λп ≈ 0,6 | hn | . |
| b |
Для пазов овального сечения (фиг. 343):
| λп = 1,25 (0,62 + | h4 | + | h1 | ). |
| s | 3b |
Для пазов круглого сечения можно найти 1
1 Е. Arnold, Wechselstromtechnik, V. 1.
| λп = 1,25 (0,62 + | h4 | ). |
| s |
