ГЛАВА XXXVI
МАГНИТНЫЕ ПОТОКИ РАССЕЯНИЯ
§ 323. Удельная магнитная проводимость потока рассеяния между головками зубцов (λz).
Кроме "пазового" потока рассеяния Фn , которому соответствует удельная проводимость паза λп(фиг. 342), необходимо еще иметь в виду поток рассеяния, замыкающийся через головки зубцов, или "зигзагообразный" поток рассеяния, как его иногда называют.
 |
 |
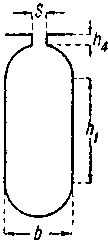
Фиг. 343. Паз овального сечения. |
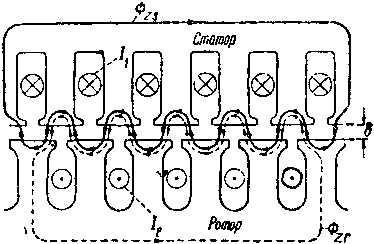
Фиг. 344. "Зигзагообразный" поток рассеяния. |
Понятие об этом „зигзагообразном" потоке дает фиг. 344. Для большей наглядности на этой фигуре предположено, что число пазов статора равно числу пазов ротора, чего на самом деле в действительности никогда не бывает, так как равенство z1 = z2 на практике не допускается во избежание затруднений при пуске двигателя в ход.
При указанном на фиг. 344 расположении зубцов ротора относительно зубцов статора под влиянием тока статора I1 и ротора I2 появятся потоки рассеяния Фzs и Фzr , которые, замыкаясь через зубцы статора и ротора, будут замыкаться по некоторым "зигзагообразным" траекториям, откуда и происходит название этого рода потока рассеяния. Для определения величины такого "зигзагообразного" потока рассеяния нет надобности рассматривать все пазы, которые в данный момент образуют потоки Фzs и Фzr, но достаточно рассмотреть один только паз, как показано на фиг. 345.
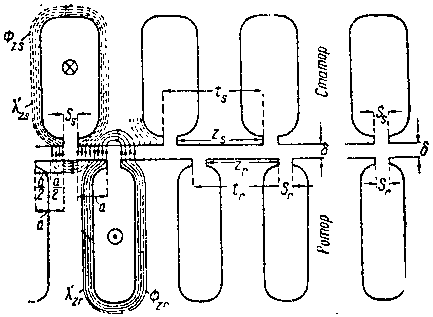 |
| Фиг. 345. Поток рассеяния между головками зубцов. |
Это положение оправдывается тем, что по мере увеличения числа пазов с проводами, создающими "зигзагообразный" поток рассеяния, соответственным образом увеличивается м. д. с., но одновременно с этим почти во столько же раз увеличивается магнитное сопротивление вследствие увеличения числа воздушных промежутков δ, через которые должен замкнуться поток рассеяния (фиг. 344). Поэтому при нахождении величины Фzs и Фzr можно рассмотреть только один паз с проводами, как показано на фиг. 345. Потоки рассеяния Фzs и Фzr колеблются 1 при вращении ротора, падая почти до нуля каждый раз, когда прорез ротора sr точно стоит против прореза ss статора.
На фиг. 345 слева показан зубец ротора, симметрично расположенный против середины прореза ss паза статора.
Найдем величину потока рассеяния между головками зубцов статора Фzs на протяжении одного сантиметра аксиальной длины, замыкающегося через головку зубца ротора
Фzs max = м. д. с. • λzs max ,
Магнитная проводимость головок зубцов при вращении ротора все время колеблется: она достигает максимального значения λzs max , когда зубец ротора находится под серединой прореза паза статора ss (см. крайний левый зубец на фиг. 345), и делается равной почти нулю, когда прорез паза ротора находится против прореза паза статора, как показано на правом чертеже фиг. 345 2.
Найдем величину λzs max на основании фиг. 345 (левый чертеж):
| a | • 1 | ||||
| λzs max = | 2 | = | a | . | |
| 2δ | 4δ | ||||
1 Эта частота колебаний соответствует частоте зубцовых гармоник.
2 Это справедливо только в том случае, когда "объем тока" статорного паза равен и противоположен "объему тока" роторного паза.
3 Это уравнение имеет приближенное значение. Точнее было бы делить отрезок а не на две равные части, как предположено в уравнении (323,1), а на части, пропорциональные q1: q2. Однако при этом формулы получились бы значительно сложнее.
Из фиг. 345 видно
2a = zr - ss = (tr - sr) - ss = tr - (ss + sr)
| а = | tr - (ss + sr ) | . |
| 2 |
Подставляем (323,2) в (323,1)
| λzs max = | a | = | tr - (ss + sr) | . |
| 4δ | 8δ |
Точно так же найдем
| λzr max = | ts - (ss + sr) | . |
| 8δ |
Как изменяются λzs и λzr в функции времени?
Обращаясь к фиг. 345, убеждаемся, что λzr и λzs практически делаются равными нулю в течение времени, соответствующего отрезку ss + sr (когда прорез паза ротора находится против прореза паза статора).
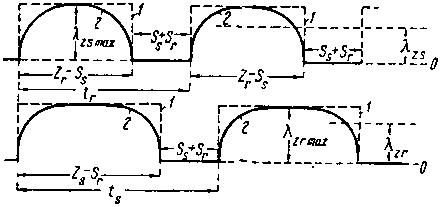 |
| Фиг. 346. Кривые изменения λzs и λzr . |
На первый взгляд может показаться, что кривые изменения λzr и λzs могут быть представлены в виде прямоугольников 1-1-1 с высотой λzs max и λzr max , отстоящих друг относительно друга на расстояниях ss + sr (см. пунктир на фиг. 346). Однако при этом необходимо иметь в виду, что при перемещении зубцов ротора величина потоков Фzs и Фzr будет периодически меняться, а следовательно, λzs и λzr будут также все время изменяться. Поэтому правильнее будет представить себе изменение магнитных проводимостей в виде кривых 2-2-2, изображенных на фиг. 346 сплошными линиями. Если бы магнитные проводимости в функции времени изображались в виде прямоугольников 1-1-1, то средние величины можно было бы найти следующим образом:
| λ''zs = λzs max ( | tr - (ss + sr) | ), |
| tr |
| λ''zr = λzr max ( | ts - (ss + sr) | ), |
| ts |
Принимая, однако, во внимание, что значения магнитных проводимостей изменяются по кривым 2-2-2, найдем более точно средние значения, умножая вышеполученные выражения на 2/3.
| λ'zs = | 2 | λzs max ( | tr - (ss + sr) | ), |
| 3 | tr |
| λ'zr = | 2 | λzr max ( | ts - (ss + sr) | ), |
| 3 | ts |
Подставляя в выражения (323,7) и (323,8) найденные выше выражения (323,3) и (323,4), найдем
| λ'zs = | [tr - (ss + sr)]2 | ; |
| 12δtr |
| λ'zr = | [ts - (ss + sr)]2 | . |
| 12δts |
Желая получить расчетную величину удельной проводимости, мы должны помножить полученные значения на 0,4π = 1,25, после чего найдем окончательно
| λzs = | 0,4π [tr-(ss + sr)]2 | ≈ | [tr - (ss + sr)]2 | ; |
| 12δtr | 10δtr |
| λzr = | 0,4π [ts-(ss + sr)]2 | ≈ | [ts - (ss + sr)]2 | ; |
| 12δtr | 10δts |
Предполагая приближенно для ориентировочных расчетов ss + sr ≈ 1/4 ts ≈ 1/4 tr и подставляя в (323,9) и (323,10), найдем
| λzs≈ | tr | ......... до | tr | ; |
| 18δ | 20δ |
| λzr = | ts | ......... до | ts | ; |
| 18δ | 20δ |
Для двигателя с открытыми пазами статора можно в формулах (323,9) и (323,10) приближенно подставить ss ≈ ts /2, после чего получится
| [tr- | ts | + sr)]2 | , | |
| λzs≈ | 2 | |||
| 10δtr | ||||
| (tr- | ts | )2 | , | |
| λzs≈ | 2 | |||
| 10δtr | ||||
| λzr = | 0,4π • ts | ≈ | ts | ; |
| 48δ | 38δ |
Сравнение формул (323,13) — (323,14) и (323,9) — (323,10) показывает, как значительно уменьшаются величины λzr и λzs при переходе на открытые пазы в статоре.
Это является (наряду с возможностью применения шаблонных секций) положительной стороной применения открытых пазов в статоре. Отрицательной стороной здесь, однако, является возрастание магнитного сопротивления воздушного зазора, что влечет за собой увеличение намагничивающего тока и понижение коэфициента мощности двигателя.
