АСИНХРОННЫЕ
МАШИНЫ

ГЛАВА VI
АСИНХРОННЫЙ ДВИГАТЕЛЬ КАК ТРАНСФОРМАТОР

§ 56. Векторная диаграмма неподвижного двигателя.

Вначале рассмотрим явления, происходящие в двигателе при неподвижном роторе.

В этом случае, как уже говорилось, такой двигатель по своему рабочему процессу ничем не отличается от трансформатора.

а)    Электродвижущие силы, индуктированные вращающимся потоком Ф в обмотках статора и ротора.

Вращающийся поток Ф будет наводить в каждой фазе статора и ротора э. д. с., эффективные значения которых соответственно равны:

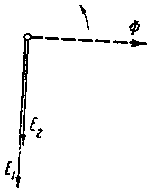
Как показано на векторной диаграмме фиг. 75, оба вектора E1 и Е2 отстают по фазе от потока Ф на угол в 90°.

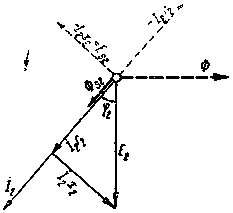Фиг. 75. Векторная диаграмма э. д. с. статора и	Фиг. 76. Векторная диаграмма э. д. с. и падения напряжений

б) Векторная диаграмма э. д. с. и токов ротора. Кроме э. д. с. Е2, наводимой в фазе обмотки ротора вращающимся потоком Ф, необходимо еще учитывать э. д. с. Es2, наводимую потоком рассеяния ротора Фs2 и активное падение напряжения.

На фиг. 76 представлена векторная диаграмма для ротора. Здесь вектор потока Ф отложен по горизонтали и вектор э. д. с. Е2—под прямым углом к Ф.

На этой векторной диаграмме еще показан вектор магнитного рассеяния ротора Фs2, отложенный в фазе с током ротора I2.

Электродвижущая сила самоиндукции Es2 или рассеяния, инуктированная потоком Фs2, отложена на фиг. 76 под прямым углом к Фs2 и отстает от него по фазе.

Величина э. д. с. самоиндукции Es2 пропорциональна роторному току I2 и может быть выражена следующим образом:

где х2 — реактивное сопротивление ротора, обусловленное потоком рассеяния.

Величина реактивного сопротивления, как известно, может быть найдена из следующего выражения:

где L2 — коэфициент самоиндукции, обусловленный потоком рассеяния ротора.

Электродвижущая сила самоиндукции Es2 представляет собой реактивную потерю напряжения. Кроме реактивной потери напряжения необходимо еще учесть активную потерю напряжения, равную

На векторной диаграмме вектор — I2r2 отложен противоположно вектору тока I2. Кроме того, на векторной диаграмме еще отложены векторы: Í2r2 в фазе с током Í2 (обратный вектору активной потери напряжения) и Í2х2, опережающий по фазе вектор тока Í2 на 90° (т. е. обратный вектору реактивной потери напряжения).

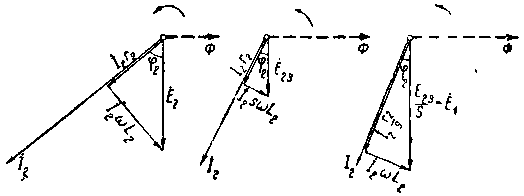Фиг. 77. Векторные диаграмммы неподвижного и вращающегося ротора.

Векторы Í2r2 и Í2х2 являются слагающими э. д. с. É2, уравновешивающими активное и реактивное падение напряжения. Иногда для краткости называют последние величины активным и реактивным   падением   напряжения.

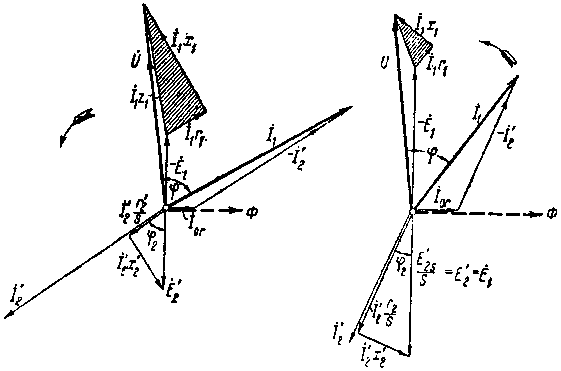Фиг. 78. Векторные диаграммы неподвижного и вращающегося двигателя.

Как видно из фиг. 76 и 77 вектор э. д. с. É2 является геометрической суммой векторов
É2 = Í2х2 + Í2r2.

Таким образом, зная положение вектора Е2 на диаграмме, мы можем найти положение вектора фазного тока ротора I2, вызываемого э. д. с. E2.

Как видно из диаграммы, ток Í2 отстает от э. д. с. É2 по фазе на угол φ2.

в) Полная векторная диаграмма (фиг. 78). Теперь обратимся к статору и попытаемся найти вектор тока в фазе статора I1 по величине и направлению (левый чертеж фиг. 78).

Если бы намагничивающий ток I0r двигателя был равен нулю, то направление вектора статорного тока I1 совпадало бы с вектором I'2. На самом деле ток I0r не равен нулю, поэтому величину статорного тока I1 придется найти на основании следующих соображений:

Вспомним, что статорный ток I1 представляет собой геометрическую разность:

Откладывая на векторной диаграмме вектор тока I0r под небольшим углом 1 к вектору потока Ф и складывая векторы Í0r и I'2, получим результирующий вектор, изображающий по величине и фазе первичный статорный ток I1.

Отложив на векторной диаграмме вектор первичного тока I1, мы можем теперь перейти к построению векторов, изображающих э. д. с. и падения напряжения в цепи статора.

В каждой из фаз этой цепи статора мы должны иметь в виду следующие величины:

1) э. д. с, индуктированную вращающимся потоком Ф;

2) активное падение напряжения;

3) реактивное падение напряжения, вызванное потоками магнитного рассеяния статорной обмотки.

Напряжение у зажимов двигателя U должно уравновешивать геометрическую сумму этих величин.

Попытаемся найти графически величину и направление вектора U, изображающую напряжение у зажимов одной фазы статора.

Отложим на векторной диаграмме вверх по вертикали (под прямым углом к вектору Ф) вектор — É1, изображающий слагающую напряжения, уравновешивающую э. д. с, индуктированную в фазе статора вращающимся потоком.

Вектор I1r1, изображающий слагающую, уравновешивающую активное падение напряжения, направим параллельно вектору I1, а вектор I1x1, изображающий слагающую, уравновешивающую реактивную потерю напряжения, — под прямым углом к I1.

Тогда, сложив геометрически векторы — Е1, Ir1 и I1x1, получим вектор напряжения у зажимов U по величине и фазе.

---

1 Обусловленными потерями на гистерезис и токи Фуко в железе статора (и отчасти ротора) двигателя.

---