ГЛАВА IV
М. Д. С. ОБМОТОК АСИНХРОННОГО ДВИГАТЕЛЯ
§ 38. Общее выражение для нахождения величин м. д. с. в любой момент времени (t) и в любой точке (х) окружности статора.
При решении задачи об изменении величины магнитной индукции в воздушном зазоре, вызываемой обмоткой, по которой течет переменный ток
(i = I sinωt), необходимо иметь в виду изменение величины м. д. с. двоякого рода:
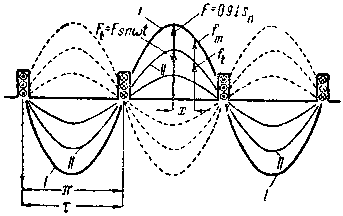 |
| Фиг. 63. Изменение основной гармоники м. д. с. фиг. 63 по времени и месту. |
а) изменение величины м. д. с. по времени: м. д. с. = φ (t);
б) изменение величины м. д. с. по месту (в различных точках окружности статора): м. д. с. = ξ (х).
а) Изменение величины м. д. с. по времени. На фиг. 63 показан ряд синусоид, которые являются первыми гармониками кривой м. д. с. в разные моменты времени t.
Жирная кривая I представляет собой 1-ю гармонику кривой м. д. с, которая получается в тот момент, когда ток, питающий обмотку, равен амплитудному значению: i = Im. Амплитуда синусоиды при i = Im, как показано на фиг. 63, будет равна: F = 0,9 • I • sn .
При уменьшении мгновенного значения тока, текущего в проводах обмотки, амплитуда синусоиды также уменьшается; в какой-нибудь момент времени t при токе i= Im •sin ωt амплитуда синусоиды будет равна (кривая II на фиг. 63)
Ft = F • sin ωt.
При токе i = 0 амплитуда кривой м. д. с. также превратится в нуль, и вместо синусоиды в этом случае мы получим прямую линию, совпадающую с осью абсцисс.
b) Изменение величины м. д. с. по месту. Обратим внимание на синусоиду, показанную на фиг. 63 жирными линиями и представляющую собой кривую распределения м. д. с. при токе
i = Im (кривая I).
На расстоянии, равном х, от амплитудной ординаты мы будем иметь величину м. д. с. fm, величина которой может быть выражена
fm = F • cos x • π/τ .
Спустя время t, ток будет меньше: i = Im • sin ωt; при этом максимальная ордината синусоиды уменьшится, как было сказано выше, до величины Ft = F • sin ωt (синусоида II).
В какой-нибудь точке окружности статора, отстоящей от максимальной ординаты на расстоянии х, величина м. д. с. при этом будет
ft = Ft • cos x • π/τ .
c) Общий вид уравнения м. д. с. Соединяя в одно уравнения (38,1) и (38,3), найдем
ft = F • sin ωt • cos x • π/τ .
Это уравнение мы можем выразить в общем виде следующим образом:
ft = ψ (t,x);
