ГЛАВА XX
КРАТКАЯ ТЕОРИЯ РОТОРА С ДВОЙНОЙ БЕЛИЧЬЕЙ КЛЕТКОЙ И С ГЛУБОКИМ ПАЗОМ
§ 200. Двигатель с глубоким пазом.
Двигатели этого типа имеют в короткозамкнутом роторе в отличие от двигателей обычных конструкций высокие и относительно узкие стержни. Высота стержней в среднем колеблется здесь в пределах 30—40 mm при толщине, равной всего 1,5—2,5 mm.
На фиг. 215 изображен стержень такого ротора с приваренным замыкающим кольцом.
Благодаря действию потока рассеяния, замыкающегося поперек паза, распределение плотности тока в высоком стержне ротора получается неравномерным, причем большая плотность тока устанавливается в волокнах провода, расположенных ближе к воздушному зазору.
Наибольшая неравномерность распределения плотности тока получается в стержнях ротора при пуске в ход, когда частота тока в роторе наибольшая. Такое "вытеснение" тока к наружному краю стержня при пуске в ход влечет за собой увеличение активного сопротивления и соответственное уменьшение реактивного сопротивления стержней ротора.
Для пояснения сказанного на фиг. 216 приведен "высокий" стержень ротора с указанием примерного распределения плотности тока в стержне при пуске в ход (кривая Sk) и при нормальной работе (кривая S).
Как видно из фиг. 216 при пуске в ход ток как бы "вытесняется" к наружному краю стержня, благодаря чему активное сопротивление стержня увеличивается.
 |
Явление такого "вытеснения" тока может быть для наглядности представлено таким образом, что рабочая часть сечения проводника при пуске в ход, когда частота тока в роторе велика, как бы перемещается кверху. Ясно, что такое "перемещение" провода к наружному краю паза должно повлечь за собой соответственное уменьшение реактивного сопротивления провода.
После того как процесс пуска в ход закончится, ротор достигнет нормальной скорости, частота токов в роторе будет небольшой, явления "вытеснения" почти исчезнут и плотность тока во всем стержне будет распределяться по высоте стержня ротора с глубоким пазом почти равномерно, как показано справа на фиг. 216 (кривая S).
Активное сопротивление rs одного стержня ротора с глубоким пазом можно представить как сумму
rs = rb + krrn ,
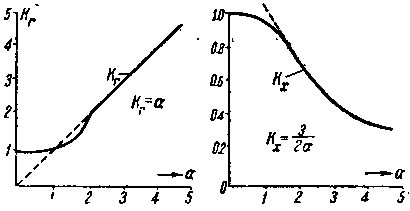 |
| Фиг. 217. Кривые изменения коэфициентов Кr и Кх в функции глубины паза. |
где rb— активное сопротивление части провода, расположенной вне железа паза (в воздухе), rn— сопротивление части провода в пазу и kr— коэфициент, больший единицы, учитывающий увеличение активного сопротивления вследствие "вытеснения". Аналогично можно написать для реактивного сопротивления xs стержня
xs = xb + kxxn,
где хп — реактивное сопротивление части провода, лежащей в пазу, xb— реактивное сопротивление части провода вне железа паза (в воздухе) и kx— коэфициент, меньший единицы, учитывающий уменьшение реактивного сопротивления под влиянием вытеснения тока.
Теория этого вопроса1 приводит к следующей зависимости, дающей возможность определения коэфициентов kr и kх в функции скольжения
1 Дана в работах Фнльда, Эмде, Роговского и К. В. Вагнера.
| kr = α | sin h2α + sin 2α | ; |
| cos h 2α— cos 2α |
| kх = | 3 | • | sin h 2α — sin 2α | . |
| 2a | cos h2α — cos 2α |
Входящая в эти формулы величина α при частоте f = 50 герц и проводах в пазах из красной меди является следующей функцией скольжения S и высоты h стержня
α = h √S.
Заметим, что при вышеуказанных условиях (f = 50 герц и при α ≥ 2), вместо сложной зависимости (200,1) и (202,2) получается более простая
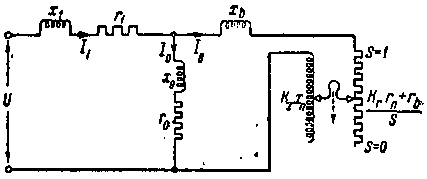 |
| Фиг. 218. Схема замещения для двигателя с глубоким пазом. |
kr = α;
| kх = | 3 | . |
| 2a |
При малых скольжениях можно положить
kr ≈ kx ≈ 1,0.
На фиг. 217 построены в виде кривых зависимости kr и kх в функции α. Из этих фигур видно, что при возрастании α (или скольжении S) kr растет, а kхуменьшается.
На фиг. 218 показана схема замещения для асинхронной машины с высокими стержнями в роторе.
Эта схема замещения отличается от таковой для обыкновенного двигателя тем, что при высоком стержне в роторе переменной величиной является не только активное сопротивление ротора, но также и реактивное сопротивление kххп .
На схеме замещения пуск и разгон двигателя может быть представлен таким образом, что ползушки реактивного и активного сопротивлений будут постепенно перемещаться книзу. При этом будет происходить постепенное увеличение реактивного сопротивления и активного сопротивления стержней ротора.
При пуске в ход (S = 1) получим
krrn = rn + (kr — 1) rn = rn + Δrn .
При малых скольжениях, когда процесс пуска в ход закончится, мы получаем kr ≈ 1 и kх ≈ 1 и, следовательно,
Δrn ≈ 0.
В момент же пуска в ход величины Δхп и Δrn достигают своего наибольшего значения. В среднем можно получить в двигателе с глубоким пазом
Δхn = 0,5хn или 0,6хn .
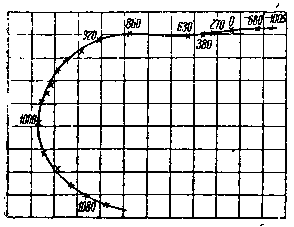 |
| Фиг. 219. Диаграмма тока двигателя с глубоким пазом на 12 kW п = 1 000 об/мин. |
Так как согласно предыдущему
kr = α = h √S,
В этом изменении rп и хп заключается коренное отличие двигателя с высоким стержнем от обычного двигателя, в котором rп и хп остаются практически неизменными при разных частотах тока. Вследствие переменности величин активных и реактивных сопротивлений обмотки ротора конец вектора тока двигателя с глубоким пазом при изменении нагрузки перемещается не по окружности как для обычного двигателя, а по кривой более сложной формы, как показано на фиг. 219.
