ГЛАВА XVIII
БЕЗРЕОСТАТНЫЙ ПУСК В ХОД АСИНХРОННЫХ ДВИГАТЕЛЕЙ С ФАЗНЫМ РОТОРОМ ПО МЕТОДУ "ПРОТИВОСОЕДИНЕНИЯ"
§ 180. Величина коэфициента взаимоиндукции.
Найдем величину коэфициента взаимоиндукции М, входящего в уравнения (5) и (6).
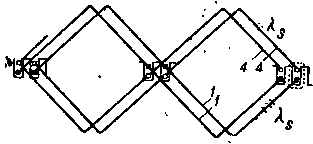 |
| Фиг. 201. Части фаз 1 и 4, соединенные по схеме фиг. 198. |
Предположим, как это бывает чаще всего, что провода фаз 1 и 4, 2 и 5, 3 и 6 соответственно лежат в общих пазах (фиг. 198). На фиг. 201 для пояснения представлены части фаз 1 и 4 обмотки; как видно из этой фигуры, соответственные провода этих фаз лежат в общих пазах один над другим. Не делая большой ошибки, можно приближенно предположить, что почти весь поток канала λп + λk (фиг. 202), создаваемый каждым из проводов, лежащих в нижней части паза, охватывает почти весь верхний проводник, и наоборот.
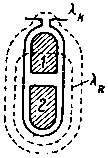 |
| Фиг. 202. Провода фаз 1 и 2, лежащие в одном пазу. |
Если бы соответственные торцевые соединения фаз 1 и 4 шли параллельно, то можно было бы предположить, что эти соединения также взаимно охватываются силовыми линиями торцевого потока рассеяния λs; на самом деле, как видно из фиг. 201 торцевые проводники соответственных фаз 1 и 4 направлены в разные стороны; поэтому приближенно можно принять
| M = | λп + λk | L = kL. |
| λп + λk+ λs |
В этом выражении λп, λk и λs обозначают магнитные проводимости потоков рассеяния на 1 cm длины ротора: паза (λп), между головками зубцов (λk) и торцевого (λs) 1.
1 О расчете этих величин см. главу XXXV.
Полученное выше приближенное выражение показывает, что величина М зависит от относительной величины λп, λk и λs; она может быть найдена для каждого частного случая, когда известны размеры паза и осевая длина ротора. Коэфициент k, входящий в уравнение (180,1), колеблется в среднем в пределах
k = 0,7—0,8.
