§ 33. Обмоточный коэфициент распределения "гладкой обмотки".

В настоящее время, как известно, обмотка обычно закладывается в пазы статора и ротора. Гладкие обмотки, при которых провода обмотки прямо укладываются по цилиндрической поверхности статора или ротора, в настоящее время совсем вышли из употребления.

Однако мы здесь все же рассмотрим случай гладкой обмотки, так как это дает нам ответ на вопрос, к какому пределу стремится обмоточный коэфициент распределения при постепенном возрастании числа пазов на полюс и фазу q.

На фиг. 61 изображена гладкая обмотка, которая занимает часть полюсного деления τ, соответствующую дуге S и центральному углу β.

При расположении проводов согласно фиг. 61 можно было бы произвести геометрическое сложение векторов, изображающих по величине и фазе э. д. с, индуктированные в проводах по методу, описанному в предыдущем параграфе.

Мы получили бы при этом правильный многоугольник с весьма большим числом сторон. Как известно, при постепенном возрастании числа сторон правильного многоугольника в пределе мы получаем окружность.

Поэтому часть многоугольника А — D — Е— С предыдущей фиг. 60 в нашем случае должна превратиться в дугу окружности ADB (фиг. 61, слева); хорда АВ при этом будет представлять собой результирующую э. д. с. Е.

Таким образом для гладкой обмотки обмоточный коэфициент распределения kр согласно фиг. 61 (слева) выразится следующим образом:

kp =	результирующая э.д.с.	=	хорда AB	.
	алгебраическая сумма э.д.с		дуга ADB

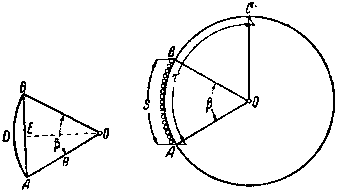Фиг. 61. Определения обмоточного коэфициента для случая гладкой обмотки.

Из прямоугольного треугольника АЕО согласно фиг. 61 (слева) найдем

AE=R•sin	β	,
	2

AB = E = 2R•sin	β	.
	2

Длина дуги ADB будет _˘АВ = R•β. Таким образом обмоточный коэфициент распределения выразится

kp =	AB (хорда)	=	2R sin(β/2)	,
	AB (дуга)		Rβ

или

kp =	sin(β/2)	.
	β/2

Так как согласно фиг. 61

β =	S	π.
	τ

то

(33.1)

kp =	sin(S/τ)•π/2	.
	(S/τ)•π/2

Подставляя в эту формулу разные значения отношения S/τ , можем найти соответственные значения обмоточного коэфициента распределения kр.

Так, например, для случая S/π = 2/3 найдем

ТАБЛИЦА 4

Значения обмоточного коэфициента распределения kp для гладкой обмотки

S/τ	kp
1 3	0,956
2 3	0,830
1 1	0,637

kp =

sin(	2	•	π	)
	3		2

sin	π
	4

= 0.830.

2	•	π
3	•	2

Если бы было S/τ = 1/3 то мы получили бы

kp =

sin(	1	•	π	)
	3		2

= 0.956.

1	•	π
3	•	2

Для S/τ = 1 найдем

kp =

sin(	1•	π	)
		2

= 0.637.

Полученные результаты сопоставлены в табл. 4.

Оглавление

Вперед

[an error occurred while processing this directive]

АСИНХРОННЫЕ МАШИНЫ

ГЛАВА III ОБМОТОЧНЫЙ КОЭФИЦИЕНТ

§ 33. Обмоточный коэфициент распределения "гладкой обмотки".

АСИНХРОННЫЕ
МАШИНЫ

ГЛАВА III
ОБМОТОЧНЫЙ КОЭФИЦИЕНТ