АСИНХРОННЫЕ
МАШИНЫ

ГЛАВА XXXVIII
ПРИМЕРНЫЕ РАСЧЕТЫ
ПРИМЕРНЫЙ РАСЧЕТ АСИНХРОННОГО ДВИГАТЕЛЯ

§ 341. Задание.

Требуется рассчитать асинхронный двигатель со следующими данными: мощность равна 42 kW (57 л. с), f = 50, U= 500 V, n1 = 1 000 об/мин, обмотка ротора фазная с кольцами, 2р = 6.

Расчет асинхронного двигателя распадается на 4 части:

A.  Выяснение размеров.

B.  Подсчет тока короткого замыкания.

C.  Подсчет тока холостого хода.

D.  Определение к. п. д.

А. Выяснение размеров
1. Сила   тока в   фазе   статора.   Примем вначале согласно ОСТ 679 приблизительно

Предполагая соединить   статорную   обмотку   в   звезду,   найдем   величину тока в фазе статора:

I1 =	kW •1 000	=	42 • 1 000	= 62,2 A
	√3U • η • cos φ		√3 • 500 • 0,9 • 0,87

Напряжение на концах одной фазы статорной обмотки будет

U  =	500	= 289 V.
	√3

Кажущаяся мощность

kWA =	kW	=	42	= 53,6.
	η cos φ		0,9 • 0,87

2. Выяснение главных размеров. На основании табл. 30 принимаем

Подставляем в основное уравнение (§ 277)

D2 • li • п1	=	5,5 • 1011	= 53,6.
kVA		k1• ai • Bl • AS

Принимая

D2li • п1	=	5,5 • 1011	,
kVA		0,72 • 0,925 • 7 800 • 330

D2li • п1	≈ 32 • 104,
kVA

или

D2 • li • 1 000	≈ 32 • 104 = С,
53,6

D2 • li  =	32 • 104 • 53,6	или D2 • li   = 17,1 • 103.
	1000

У нас получилось одно уравнение с двумя неизвестными: D и li  Такое уравнение допускает бесконечно большое число решений. Из всех этих решений нам необходимо выбрать одно, дающее наилучшее решение задачи как с конструктивной, так и с точки зрения стоимости машины. Задаваясь различными значениями D в полученном выше уравнении, найдем соответственные значения li  и занесем результат подсчетов в табл. 42.

ТАБЛИЦА 42

№	D (cm)	li (cm)	τ = πD/2p(cm)	v (m/sec)	li /τ
1	29	20,5	15,2	15,2	1,36
2	31	17,8	16,2	16,2	1,10
3	33	15,8	17,3	17,3	0,92
4	35	14,0	18,3	18,3	0,77

1 Величина ai в современных машинах изменяется от 0,69 до 0,72 в зависимости от насыщения. Большая величина ai взята вследствие относительно большого насыщения.

---

Выберем вариант № 2 с данными:

3. Осевая   длина.   Возьмем   3   вентиляционных   промежутка    (ns = 3) по 1 cm шириной каждый. Осевая длина будет

Кроме того,

откуда

Длина каждого железного пакета будет

Таким образом

4. Воздушный зазор. Формула Пихельмайера дает

Из формулы Каппа следует

Если бы мы обратились к кривой фиг. 331, то мы бы нашли другую величину:

Остановимся окончательно на средней величине, соответствующей ОСТ 679,

Последняя величина находится в согласии с данными табл. 27. 5. Число   пазов   в   статоре.   Выбрав число пазов на полюс и фазу q1 = 4, найдем общее число пазов

Зубцовое деление будет

ts =	πD	=	π • 31	= 13,5 mm.
	z1		72

Выбрав число пазов zl , проверим,   не   получится   ли   при этом чрезмерно большое значение объема тока в пазу In ; имеем

Большая величина In неблагоприятно отзывается на cos φ, так как при больших значениях In реактанц обмоток, вызванный магнитным рассеянием, увеличивается, и ток короткого замыкания   Ik понижается. Величина   Iп = 445 для нашего случая допустима.

---

1 Величина In обычно колеблется в пределах от 400 (малые машины) до 800  (большие машины) и редко превосходит величину 1000 А.

---

6. Число    проводов    в    пазу    статора.   Найдем число проводов в одном пазу

sn =	ts • AS • a1	,
	I1

a1— число параллельных цепей фазной обмотки.

Выберем a1 = 4. Это дает возможность произвести более компактную укладку проводов в пазу и позволит уменьшить ширину прорези у паза, через которую производится укладка обмотки (Ss = 2,5 ÷ 3,5 mm), что скажется на увеличении cos φ:

sn =	1,35 • 330 • 4	= 28,6.
	62,2

Округляя, выберем окончательно

7. Число   последовательно   соединенных витков   в   фазе статора.   Найдем из формулы

w1 =	sn • p • q	=	28 • 3 • 4	= 84 витка..
	a1		4

8. Плотность тока в проводах статора. Так как нагрев статора пропорционален произведению AS • sa (§ 288), то плотность тока приходится брать меньше в тех случаях,   когда линейная нагрузка AS велика.

Плотность тока рекомендуется выбирать с таким расчетом, чтобы было соблюдено следующее условие:

Из последнего неравенства найдем

sa =	1000	до	2 200	;
	AS		AS

sa =	1000	—	2 200	= 3,7 - 6,7.
	330		330

Имея в виду   также   данные   табл.   30  на  стр.  319,   окончательно   остановимся на следующей величине плотности тока в обмотке статора:

9. Сечение проводов статора

Так как число параллельных цепей a1 = 4, сечение одного   провода получится 12,4/4 = 3,1 mm2. Выбираем по ОСТ 4123   круглую   проволоку   ПБД  диаметром в   1,95   mm   (сечением,   равным   2,99   mm2);   диаметр проволоки с изоляцией d1 = 2,2 mm.

Общее сечение проводов фазы статора будет

Плотность тока изменится и будет равна

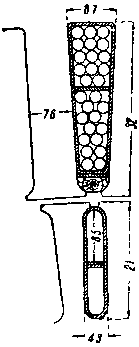Фиг. 384.

Обмотку статора выполняем в виде двухслойной с укороченным шагом, так называемыми "мягкими секциями". Секции выполняются на шаблоне без общей изоляции и "насыпаются" в паз через щель паза ss.

Ширина щели паза

Шаг обмотки

y = τβ =	z1	•β,
	2р

где τ — полюсное деление, выраженное в зубцовых делениях; β — укорочение шага, равное

отсюда

y =	72	• 0,8 = 9,6,
	6

выбираем тогда

β =	10	= 0,835.
	12

10. Размеры паза. Форму паза выбираем трапециевидную. Число проводов в пазу 28. Изоляцию паза выполняем из двух слоев прессшпана по-0,2 mm и одного слоя микаленты в 0,2 mm, помещаемой между слоями прессшпана.

Необходимая наибольшая ширина паза определится следующим образом: считаем, что в наиболее широкой части паза укладываются три ряда проводов. Остальные провода размещаем согласно фиг. 384, откуда наибольшая ширина паза будет:

1. Три медных провода диаметром d1 = 2,2 mm, всего ширина 2,2 X 3 = 6,6 mm.

2.   Изоляция паза:

 

Допуск на укладку                                                                                       = 1,3 mm

---

                                                                                 Итого   = 8,7 mm

Высота паза определится следующим образом:

1. 12 рядов проволоки (d1= 2,2 mm)                                                            2,2 • 12 = 26,4 mm
2. Изоляция паза                                                                                               0,6 •  2 = 1,2 mm
3. Прокладка между секциями из промасленного полотна 3 слоя по 0,2             = 0,66 mm
4. Клин                                                                                                                          = 2,5 mm
5. Высота прореза                                                                                                         = 0,5 mm
6. Допуск на укладку                                                                                                     = 0,8 mm

---

                                                                                                                Итого    = 32 mm

Максимальная ширина зубцового деления статора

tsmax =	π (D + hs • 2)	=	π (31 + 2 • 3,2)	= 16,3 mm.
	z1		72

Ширина зубца

Средняя величина зубцового деления статора будет

tsm =	π (D + hs)	=	π (31 + 3,2)	= 14,9 mm.
	z1		72

Остальные размеры определяются по фиг. 384. Отношение

zs	=	7,6	= 0,51.
tsm		14,9

Коэфициент заполнения паза будет

2,99 • 28		= 0,363.
8,7 + 5,8	• 32
2

Фиг. 385.

11. Обмотка ротора. (Выполнение в виде трехфазной обмотки с контактными кольцами.)   Число   пазов   на   полюс и фазу в роторе q2   не должно быть равно q1 во избежание явления "прилипания" при пуске в ход; поэтому q2 возьмем больше чем q1; так как для статора мы выбрали q1 = 4, то для ротора возьмем q2 = 5.

Выберем стержневую двухслойную обмотку с двумя стержнями в пазу (sn = 2); число витков одной фазы в этом случае будет

Для того чтобы убедиться в том, правильно ли нами выбрано число витков w2, найдем величину напряжения в фазе ротора, когда двигатель неподвижен:

E2 = U•	w2 • k2	.
	w1 • k1

Здесь k2 и k1— обмоточные коэфициенты, определяемые следующим образом:

здесь 0,958 — обмоточный коэфициент распределения, определяемый из уравнения

sin ( π ) 2m1	=	sin ( π ) 2 • 3	= 0,958;
q1sin ( π ) 2m1q1		4 sin ( π ) 2 • 3 • 4

0,966 — коэфициент "укорочения", учитывающий укорочение    шага   обмотки, определяется из уравнения

sin	y	• 90° = sin	10	• 90° = 0,966.
	τ		12

Обмотка ротора выполнена волновой обходной и не имеет укорочения шага, поэтому

k2 =	sin ( π ) 2m2	=	sin ( π ) 2 • 3	= 0,957;
	q2sin ( π ) 2m2q2		5 sin ( π ) 2 • 3 • 5

Электродвижущая сила ротора будет

Е2 = 289	30•0.957	= 107 V.
	84•0.925

(В двигателях средней мощности обычно допускаемое напряжение между контактными кольцами колеблется в пределах 100 — 200 V 1.)

---

1 Для машин большой мощности приходится допускать большие значения 500 — 800 — 1 000 V.

---

12. Величина тока в фазе ротора. Предполагая приближенно, что ампервитки статора больше ампервитков ротора примерно на 15%, можно найти величину нормального тока в роторе

I2 = 0,85 •	I1k1m1w1	= 0,85	62,2 • 0,925 • 3 • 84	= 142 A.
	k2m2w2		0,957 • 3 • 30

13. Число   пазов   ротора

14. Зубцовое деление ротора

tr =	πDr	=	π (310 — 2 •0.6)	= 10,8 mm.
	z2		90

15.  Сечение   проводов   ротора.  Выберем  такую   форму   сечения проводов ротора, чтобы ширина паза ротора была немного меньше половины зубцового деления 10,8/2 = 5,4; остановимся на ширине паза равной 4,3.

Изоляция паза по ширине состоит из:

Найдем, что ширина меди проводов может быть равной

Сечение провода qа2 найдем, задавшись плотностью тока

qа2 =	I2	=	142	=23,7.
	sa2		6

Выберем провод фасонного сечения 2,8X8,5  согласно   фиг.   384.  Сечение этого провода будет немного меньше, чем полученное выше — 23,5 mm2. Произведем обратную проверку на плотность тока

16. Размеры паза ротора. Ширина паза определится следующим образом:

Ширину прореза паза берем

Максимальная величина зубцового деления ротора

Максимальная ширина зубца

Минимальная ширина зубцового деления ротора

tr min =	π (D — 2δ - 2rh)	=	π (310 — 2 • 0,6 — 2 • 21)	= 9,35 mm.
	z2		90

Минимальная ширина зубца ротора

Средняя величина зубцового деления ротора будет

trm =	tr max + tr min	=	10,8 + 9,35	= 10,1 mm.
	2		2

Найдем среднюю ширину зубца ротора

17. Величина магнитного потока

Ф =	Е1• 108	.
	4,44k1• f1• w1

Принимая приближенно

получим поток

Ф =	0,97 • 289 • 108	= 1,62 • 106.
	4,44 • 0,925 • 50 • 84

18.  Высота  сердечника   статора  (hs). Средняя величина магнитной индукции в сердечнике статора будет (фиг. 334).

Bs =	Ф	.
	2lhsk2

откуда

hs  =	Ф	.
	2lk2Bs

Задаваясь Bs = 12 000 и принимая коэфициент k2 (учитывающий   влияние изоляционных лаковых прослоек между листами) равным 0,95, найдем

hs  =	1,62 • 106	≈ 4,35 cm.
	2 • 16,5 • 0,95 • 12 000

19. Высота сердечника ротора (hr). При выборе размера hr задаемся средней величиной магнитной индукции в железе ротора Вr; при этом мы можем выбрать магнитную индукцию в роторе Вr больше чем для статора, так как скорость вращения ротора нормально почти равна скорости вращающегося потока, вследствие чего потери на гистерезис и токи Фуко в железе ротора очень невелики.

Задаваясь Вr = 12 500, найдем

hr  =	Ф	=	1,62 • 106	≈4,2 cm.
	2l • k2 • Вr		2 • 16,5 • 0,95 • 12 500

20. Внешний  диаметр  железа  статора (фиг. 322)

Округляем

21. Внутренний диаметр железа ротора (фиг. 322)

22. Диаметр вала найдем на основании формулы

d = 10 4	√	PS	= 19 4	√	57	≈ 95 mm.
		n			1000

В. Ток короткого замыкания

23.  Активное   сопротивление  статорной  обмотки. Сопротивление одной фазы при постоянном токе будет равно:

rg =	2w1la1	•	[1 + 0,004T]	.
	a1		5 700 • qa1

Средняя длина полувитка будет

Кроме того, Таким образом

r1g =	2 • 84 • 44	•	[1 + 0,004 • 55]	= 0,132 Ω.
	4		5 700 • 2,99

Действительная   величина   активного   сопротивления   (с   учетом    влияния "кожного эффекта") будет больше чем rg . Приблизительно можно принять

24. Активное сопротивление роторной обмотки. Сопротивление одной фазы при постоянном токе

r2g =	2w2	•	[1 + 0,004 T]	,
	a2		5 700 • qa2

где

r2g =	2 • 30 • 44	•	1.22	= 0,024 Ω.
	1		5 700 • 23,5

Вследствие малой частоты тока в роторе сопротивление при переменном токе (при нормальном числе оборотов   ротора)   считаем   равным   активному,

Приведенное значение сопротивления одной фазы ротора

r'2 =	m1w12k12	r2,
	m2w22k22

r'2 =	3 • 842 • 0,9252	• 0,024 = 0,175 Ω.
	3 • 302 • 0,9572

25. Суммарное активное сопротивление при коротком замыкании

Падение напряжения в активном сопротивлении

eR% =	I1r1	• 100 +	I2r2	• 100;
	U1		U2

eR% =	62,2 • 0,139	• 100 +	142 • 0.024	• 100;
	289		107

26. Удельная проводимость магнитного рассеяния статорной обмотки (λ1) и роторной (λ2). Эти величины найдем по формуле (§ 327).

λ1 = kn • 0,6	hns	+	tr	+ 0,4	τq1	для статора
	bns		18δ		li

λ2 = kn • 0,6	hnr	+	ts	+ 0,4	τq2	для ротора
	bnr		18δ		li

kn — коэфициент, учитывающий уменьшение магнитного рассеяния от укорочения шага обмотки; для статора имеем

kn =	3β + 1	=	3 • 0,835 + 1	= 0,875.
	4		4

Для ротора kn = 1 (так   как   стержневую обмотку ротора  выполняем без укорочения шага) 1.

---

1 Обычно волновые обмотки ротора имеют диаметральный шаг. Сокраще­ние шага в роторных волновых обмотках не приводит к сокращению длины лобовых частей, так как сокращение первого частичного шага приходится компенсировать соответственным удлинением второго частичного шага.

---

На основании чертежа пазов (фиг. 384) заполним табл. 43.

ТАБЛИЦА 43

	Статор	Ротор
Высота паза	hns = 32 mm	hnr = 21 mm
Ширина паза	bns = bms = 7.3mm (средняя величина)	bnr = 4,3 mm
Зубцовое деление kn q1 q2	ts = 13,5 mm 0,875 4 -	tr = 10,8 mm 1 - 5

Подставляя в вышенаписанные формулы данные этой таблицы, найдем

λ1 = knλn + λz + 0,4	τq1	= 0,875 • 0,6	32	+	10,8	+ 0,4	16,2 • 4	= 4,86;
	li		7.3		18 •0.6		18

λ2 = λn + λz + 0,4	τq2	= 0,6	21	+	13.5	+ 0,4	16,2 • 5	= 6.13;
	li		4.3		18 •0.6		18

27. Реактанц одной фазы статорной обмотки. Найдем на основании формулы

x1 =	4πf1w12	λ1 • li.
	pq1 •108

Подставив в вышенаписанную формулу:

найдем

x1 =	4πfw12	λ1li =	4π50 • 842	• 4,86 • 18 = 0,325 Ω.
	pq1108		3 • 4 • 108

28. Реактанц фазы роторной обмотки

x2 =	4πfw22	λ2li .
	pq2108

Подставляя в эту формулу:

найдем

x2 =	4πfw22	λ2li =	4π50 • 302	• 6.13 • 18 = 0,0415 Ω.
	pq2108		3 • 5 • 108

Приведенная величина

x'2 =	m1	(	w1k1	)2  x2 =	3 • 842 • 0,9252	• 0,0415 = 0,305 Ω.
	т2		w2k2		3 • 302 • 0,9572

29.   Суммарное   значение   реактанца   при   коротком   замыкании

Падение напряжения в реактивном сопротивлении в процентах

eх% =	I1х1	100 +	I2х2	100 =	62,2 •0.325	100 +	142 • 0,0415	100 = 7,0 + 5,5 = 12,5%.
	U1		U2		289		107

30. Импеданц   короткого   замыкания

31. Ток короткого замыкания

Ik =	U	=	289	= 415 А.
	zk		0.7

32. Коэфициент мощности при коротком замыкании

cos φk =	rk	=	0,314	= 0,45.
	zk		0.7

33. Отношение тока короткого замыкания к нормальному

Ik	=	415	= 6,7.
I1		62,2

С. Ток холостого хода

34.   Ампервитки, необходимые для создания магнитного потока,   складываются   из:

AWl(воздушные ампервитки);
AWzs("зубцовые" ампервитки в статоре);
AWzr(зубцовые ампервитки в роторе);
AWs(ампервитки в сердечнике статора);
AWr(ампервитки в сердечнике ротора).

35. Ампервитки воздушного промежутка. Максимальное значение магнитной индукции в воздушном зазоре будет

Bl =	Ф	=	1,62 • 106	= 7 700.
	aiτli		0,72 • 16,2 • 18

Величина Bl у нас получилась меньше, чем та, из которой мы исходили в наших расчетах (Bl = 7 800), потому что при выборе li мы округлили li в большую сторону.

Найдем расчетную величину воздушного промежутка где

где

kδ = (	ts + 10δ	)(	tr + 10δ	).
	zs + 10δ		zr + 10δ

Подставляя   в   вышенаписанную   формулу: δ = 0,6 mm, ts= 13,5 mm, zs = 13,5 — 3,0 = 10,5 mm, tr = 10,8 mm,  zr = 10,8—1,5 = 9,3 mm, найдем

kδ = (	13,5 + 10 • 0,6	) • (	10,8 + 10 • 0,6	) =	19,5	•	16,8	= 1,29.
	10,5 + 10 • 0,6		9,3 + 10 • 0,6		16,5		15,3

Таким образом расчетная длина воздушного промежутка

Найдем ампервитки воздушного промежутка

36. Зубцовые ампервитки статора. Найдем магнитную индукцию в зубце статора

Вzs =	ts • Вl • li	=	13,5 • 7 700 • 180	= 15 700.
	k2 • zms • l		0,95 • 7,6 • 165

По кривой намагничивания фиг. 335 найдем для этого значения магнитной индукции соответственное число "удельных" ампервитков

Общее число ампервитков, приходящееся на пару зубцов статора, будет

37. Зубцовые ампервитки ротора. Минимальная величина индукции в зубце ротора

Вz min=	tr • Вl • li	=	10,8 • 7 700 • 180	= 14 600.
	k2 • zr max • l		0,95 • 6,5 • 165

Средняя величина индукции в зубце  ротора

Вz m=	tr • Вl • li	=	10,8 • 7 700 • 180	=16 400.
	k2 • zr m • l		0,95 • 5,775 • 165

Максимальная величина индукции в зубце ротора

Вz max=	tr • Вl • li	=	10,8 • 7 700 • 180	=18 850.
	k2 • zr min • l		0,95 • 5,05 • 165

По кривой фиг. 335    найдем   соответствующие   этим индукциям удельные ампервитки

Расчетные удельные ампервитки

awr =	awr min + 4awrm + awr max	=	20 + 4 • 45 + 210	= 68.
	6		6

Общее число "зубцовых" ампервитков ротора будет

38. Ампервитки железа статора. Средняя длина пути магнитны линий потока в железе статора

Ls ≈ π •	D1 - hs	= π	46,5-4.35	= 22 cm.
	2p		6

По кривой намагничивания (фиг. 335) для Bs = 12 000 найдем

Суммарные ампервитки

39. Ампервитки железа ротора. Средняя длина пути магнитных линий в железе ротора (фиг. 334)

Lr =	π •(D2 + hr)	= π	85 + 32	= 12 cm.
	2p		6

По кривой намагничивания (фиг. 335) для Вr = 12 500 найдем

Суммарные ампервитки

Сумма ампервитков

Найдем отношение

AW0	=	1735	= 1,86.
AWl		955

41. Намагничивающий ток (реактивная слагающая тока холостого хода).   Согласно § 305 будет

Ior =	1,11p •  AW0	=	1,11 • 3 • 1 735	= 24,7.
	m1 • w1• k1		3 • 84 • 0,925

Ior% =	Ior	100 =	24,7	100 = 39%.
	Il		62,2

Найдем отношение

Il	=	62,2	= 2,18.
Ior		24,7

42. Вес   железа   статора (фиг. 322). Вес железа статора (без зубцов)

Ps = 22l [(	D1	)2 - (	D	+ hns)2]10-3 kg = 22 • 16,5 [(	46,5	)2 - (	31	+ 3,2)2] 10-3 = 69 kg.
	2		2		2		2

Вес зубцов статора

43. Потери на гистерезис и токи Фуко, отнесенные к 1 kg веса, в железе статора (без зубцов)

vs = vhs + vfs = [ε	f	+ σ (	f	)2](	Bs	)2.
	100		100		10 000

Статор выполним из листов "динамного" железа толщиной Δ = 0,5 mm. Подставим в вышенаписанную формулу для f = 50 на основании   таблицы § 99 следующие значения:

Подставляя в вышенаписанную формулу Bs = 12 000, найдем

vs = [4,4	50	+ 5.6 (	50	)2](	12000	)2 = 3,6 • 1,44 = 5,18 W.
	100		100		10000

44. Потери железа в сердечнике статора. Найдем по формуле

где k — коэфициент, учитывающий влияние механической обработки железа на потери; приближенно приняв k = 2 (§ 88), найдем

45. Потери на гистерезис и токи Фуко, отнесенные к 1 kg веса, в зубцах статора

vz = vhz + vfz = [ε •	f	+ σ (	f	)2](	Bzs	)2,
	100		100		10000

vz = 3,6 (	15 700	)2 = 8,9 W.
	10 000

46. Потери железа в зубцах статора

47. Потери на трение и вентиляцию оценим приближенно в 1,5% от мощности

48. Пренебрегая джоулевыми потерями, найдем величину суммарных потерь холостого хода

49. Активная слагающая тока холостого хода

I0a =	V0	=	1705	= 1,96 A.
	m1U		3 • 289

50. Ток холостого хода

51. Коэфициент мощности при холостом ходе

cos φ0 =	I0a	=	1.96	= 0,0.8.
	I0		24.7

52. На основании имеющихся данных можно построить круговую диаграмму. В результате графически из круговой диаграммы1 можно   найти для нормального тока I1 = 62,2 А следующие величины:

---

1 Круговую диаграмму можно построить по способу, указанному в § 150.