ГЛАВА X
КРУТЯЩИЙ МОМЕНТ
§ 88. Зубцовые поля и влияние их на форму кривой крутящего момента и на шум машины.
1. Зубцовые магнитные поля. Действительные кривые крутящих моментов совпадали бы с кривыми, полученными из круговых диаграмм (согласно фиг. 90), только в том случае, если бы мы имели дело с синусоидальным распределением магнитной индукции в воздушном зазоре.
В действительности же мы имеем всегда дело с более или менее искаженными по форме кривыми магнитных полей.
Главной причиной искажения формы кривой магнитной индукции в воздушном зазоре являются зубцы статора и ротора.
Благодаря наличности зубцов кривая распределения магнитной индукции в воздушном зазоре теряет свой синусоидальный характер. На фиг. 97 представлена такая примерная кривая магнитной индукции — III. Если бы зубцов не было ни в статоре, ни в роторе, то мы бы имели синусоидальное распределение согласно кривой I. Благодаря наличию зубцов в статоре на основную гармонику I накладываются высшие гармоники II, вызванные зубцами, в результате чего получается кривая III.
Фиг. 97 относится к тому случаю, когда зубцы имеются только в статоре и когда ротор имеет совершенно закрытые пазы.
При открытых (или полуоткрытых) пазах в роторе кривая магнитной индукции получается еще более сложной.
Из вышеизложенного видно, что при проектировании двигателя с короткозамкнутым ротором чрезвычайно важным является выбор надлежащего числа пазов в роторе и статоре.
При неправильном сочетании числа пазов статора и ротора в кривой магнитного потока появляются высшие гармоники, оказывающие вредное влияние на форму кривой крутящего момента двигателя при его разбеге.
2. Крутящие моменты, создаваемые высшими гармониками. Магнитные зубцовые поля вращаются в пространстве с меньшей скоростью, чем магнитные поля основной гармоники.
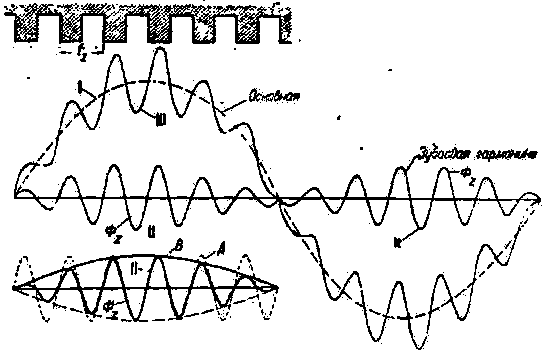 |
| Фиг. 97. Зубцовые гармоники. |
Число оборотов какого-нибудь поля v-го порядка, имеющего vp пар полюсов, будет равно
| nv = | 60f | = | n1 | . |
| vp | v |
Таким образом, например в двухполюсном двигателе, для которого при f = 50, мы имеем п1 = 3 000 об/мин, найдем число оборотов в 1 мин. магнитного поля 7-го порядка:
| 3000 | = 429 об/мин | . |
| 7 |
Крутящий момент, создаваемый двигателем, будет вообще складываться из крутящего момента, создаваемого основной гармоникой
М1 = kB1I21cos φ1,
Mv = k1BvI2v cos φv 1.
1 В двух последних выражениях означают: I21 — основная (первая) гармоника роторного тока, I2v — v-тая гармоника роторного тока.
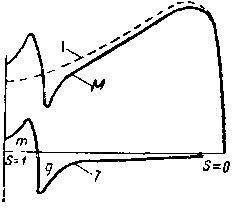
На фиг. 98 показана кривая изменения крутящего момента М для двигателя с сильно развитыми зубцовыми полями, дающими гармонику 7-го порядка в кривой поля.
Если бы высших гармоник в кривой магнитного поля не было, то мы имели бы кривую моментов I. Благодаря наличности, однако, 7-й гармоники появляется дополнительный момент в виде кривой 7 (фиг. 98).
При скорости ротора, меньшей чем n1/7, дополнительный момент имеет положительное значение (т на фиг. 98) и складывается с моментом от основной гармоники. При скорости ротора, равной n1/7, ротор вращается синхронно с магнитным полем 7-й гармоники, и поэтому дополнительный момент при этих условиях равен нулю.
При скорости, большей n1/7,получается генераторный тормозящий момент (g — на фиг. 98).
 |
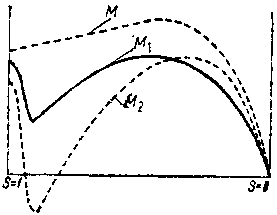 |
| Фиг. 98. Кривая изменения крутящего момента М для двигателя с сильно развитой седьмой гармоникой. | Фиг. 99. Влияние зубцовых гармоник на кривые крутящих моментов. |
Таким образом в результирующей кривой M получается впадина, при достаточной глубине которой может случиться, что ротор при нагрузке машины не в состоянии будет развить нормальное число оборотов: произойдет "застревание" ротора на скорости значительно меньше нормальной.
Эти высшие гармонические могут иногда получать такое большое значение, что кривая крутящих моментов при некоторых скоростях ротора будет лежать в области отрицательных ординат, как показано на фиг. 99 (кривая М2). Такой двигатель не может самостоятельно раскрутиться до нормальной своей скорости и поэтому не может быть признан доброкачественным.
3. Влияние числа зубцов ротора. Мы видим из вышеизложенного, что в случае наличия зубцовых полей в кривой поля мы будем по существу иметь в одной машине не один, но как бы несколько двигателей: один двигатель с числом полюсов 2p и синхронной скоростью поля, равной n1, и ряд других двигателей с числом полюсов 2pv и синхронными скоростями n1/v, где v — порядок высшей гармоники.
На фиг. 98 показана кривая крутящего момента М при наличности высшей гармонической — 7-й.
Однако известны случаи, когда появляются гармоники 13-я, 19-я и т. д.
Появление высших гармоник, искажающих кривую крутящих моментов, связано с тем или другим соотношением числа зубцов в статоре и роторе.
Опыт и теория показывают, что имеется возможность так подобрать число зубцов в статоре и роторе, при которых можно избежать искаженных форм кривой крутящих моментов.
На фиг. 100 изображена приближенная кривая зубцовых полей, накладывающаяся на основную гармонику (не показанную на фиг. 100).
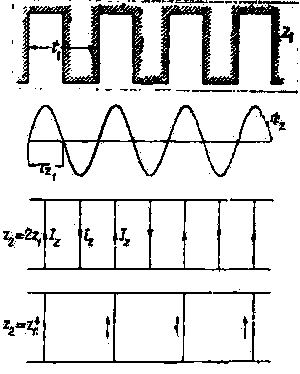 |
| Фиг. 100. Кривая зубцовых полей. |
Если в статоре двигателя число пазов будет равно zl, а в роторе число пазов будет вдвое больше, чем в статоре, т. е. z2 = 2z1, то, как видно из фиг. 100, в этом случае в беличьем роторе появятся добавочные токи Iz, вызванные зубцовыми полями, которые будут стремиться затормозить ротор, который не сможет при этих условиях самостоятельно развернуться до нормальной скорости.
Таким образом отсюда видно, что соотношение z2 = 2z1 является весьма неблагоприятным и должно поэтому быть избегаемо.
Если в роторе взять число пазов так, чтобы
z2 = zl, в этом случае зубцовые потоки Фz не вызовут в обмотке ротора никаких добавочных токов, так как э. д. с, индуктированные в стержнях ротора, будут взаимно компенсированы, как показано стрелками на нижнем чертеже фиг. 100.
Таким образом на первый взгляд может показаться, что наиболее благоприятным соотношением зубцов статора и ротора с точки зрения хороших пусковых свойств является
z2 = z1. Однако выполнение последнего условия приводит нас к конфликту с требованием устранения явления "прилипания", которое резче всего появляется при z2 = z1.
Для выхода из этого затруднения приходится при выборе числа пазов в роторе руководствоваться целым рядом добавочных условий, о которых говорится ниже.
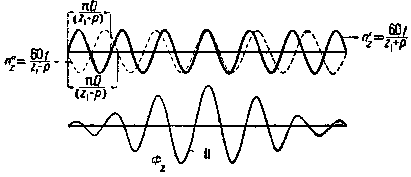
4. Порядок высших зубцовых гармоник. Рассмотрим кривую зубцовых полей Фz, построенную на протяжении одного полюсного деления (фиг. 101).
Кривая изменения зубцового потока Фz, изображенная выше, на фиг. 100, имеет грубо приблизительный характер. Действительная же кривая изменения зубцового потока Фz имеет другой вид, как показано на фиг. 101. Из этой фигуры видно, что амплитуда колебаний магнитной индукции достигает максимального значения в том месте, где магнитная индукция в воздушном зазоре основной гармоники достигает максимального значения и постепенно уменьшается по мере приближения к тем местам воздушного зазора, где основная гармоника переходит через нулевое значение.
Таким образом кривая изменения Фz в действительности имеет характер кривой "биения" или "интерференционной" кривой.
Такая кривая, как известно, может быть представлена как результат сложения ординат двух синусоидальных кривых разной периодичности, вращающихся в пространстве в противоположные стороны.
Обозначив через v'z и v"z порядок этих двух синусоид, найдем число оборотов этих двух вращающихся в противоположные стороны синусоид:
n'z = n1/v'z ("прямое" поле),
n''z = n1/v"z ("инверсное" поле).
При этом порядок гармоник будет
v'z = z1/p + 1 = 2mq + 1,
v"z = z1/p - 1 = 2mq - 1,
Таким образом найдем
| n'z = | n1 | = | 60f | ("прямое" поле) |
| z1/p +1 | z1 + p |
| n"z = | n1 | = | 60f | ("инверсное" поле) |
| z1/p -1 | z1 - p |
Фиг. 101. "Интерференционная" кривая сложения "прямой" и "обратной" гармоник. |
 |
5. Полюсное деление зубцовых гармоник. Если бы кривая зубцового поля Фz имела характер синусоиды с постоянной амплитудой, как показано на фиг. 100, то величину полюсного деления τz1, "зубцовой" кривой мы нашли бы равной половине зубцового деления t1:
| τz1 = | t1 | = | πD | . |
| z | 2z1 |
Однако, как было сказано, кривая зубцового потока Фz на самом деле имеет более сложную форму, чем на фиг. 100, представляя собой "интерференционную" кривую фиг. 101, которая в свою очередь может быть рассматриваема как результат сложения двух бегущих в противоположные стороны гармоник— "прямой" и "инверсной". Найдем полюсные деления этих гармоник:
τ'z = τ/v'z
τ"z = τ/v"z
Порядок этих гармоник равен
| v'z = | z1 | +1 и v"z = | z1 | - 1 1. |
| p | p |
Имея в виду соотношения
| τ = | πD | , |
| 2р |
| τz1 = | πD | , |
| 2z1 |
| τ'z = | τ | = | τ | = | τр | = | πD |
| v'z | z1/p + 1 | z1 + p | 2(z1 + p) |
| τ"z = | πD |
| 2(z1 - p) |
На основании (88,1) последние выражения перепишем:
| τ'z = τz1 | z1 | ("прямое" поле), |
| z1 + p |
| τ''z = τz1 | z1 | ("инверсное" поле). |
| z1 - p |
Для наглядности все полученные выше соотношения сопоставлены в табл. 11.
ТАБЛИЦА 11
| "Прямое" поле | v'z = z1/p + 1 = 2mq + 1, |
|
|
|||||||||
| "Инверсное" поле | v"z = z1/p - 1 = 2mq - 1, |
|
|
1 См. статью Моллера (Möller) в "Archiv für Elektrotechnik." — "Ueber Drehmomente beim Aulauf von Drehstrommotoren mit Köfigaukern".
Предполагая т = 3, найдем на основании вышеприведенных формул порядок высших гармоник для разных значений q:
|
q | 1 | 2 | 3 | 4 |
| "Прямое" поле | vz' | 7 | 13 | 19 | 25 |
| "Инверсное" поле | vz'' | 5 | 11 | 17 | 23 |
На основании этой таблицы следует, что "прямая" гармоника поля статора с полюсным
| делением, равным | πD | , не будет наводить в проводах ротора никаких э. д. с., при условии, |
| 2(z1 + p) |
z2 ≈ 1,25 (z1+ p).
Для уменьшения реактанца роторной обмотки можно в случае необходимости отступать от этого правила, выбирая согласно Моллеру большее число пазов в роторе, однако, с таким расчетом, чтобы
z2< (1,7 - 1,8)z1.
1 См. статью Б. П. А п а р о в а, "Электричество" № 8, 1932.
6. Синхронный момент, вызываемый высшими гармониками. Опыт показывает, что при известном соотношении числа пазов в статоре и числа пазов ротора в виде беличьей обмотки ротор может устойчиво вращаться с синхронно-постоянной скоростью, меньшей, чем скорость вращающегося потока основной гармоники.
Как показывает теория, в кривой распределения магнитной индукции вращающегося потока, создаваемого трехфазной обмоткой, обычно имеется ряд высших гармонических, нечетных и неделящихся на 3. При этом гармоники порядка 7-го, 13-го, 19-го и т. д. дают потоки, вращающиеся в положительную сторону, и гармоники 5-я, 11-я, 17-я и т. д. дают потоки, вращающиеся в сторону, противоположную вращению первой гармоники (так называемые "инверсные" поля).
Гармоники поля одного и того же порядка в статоре и роторе при определенных скоростях могут вступить во взаимодействие, в результате чего может появиться при этих скоростях синхронизирующий момент.
Сказанное поясняет фиг. 102.
На этой фигуре изображены основная гармоника потока, вращающаяся со скоростью, равной п1, и одна из высших гармоник, имеющая в v раз больше полюсов: она вращается со скоростью, равной n1/v, т. е. со скоростью в v раз меньшей, где v — порядок гармоники (кривая А на фиг. 102).
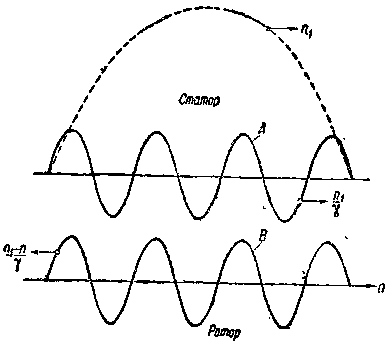 |
| Фиг. 102. Чертеж, поясняющий возникновение синхронных моментов от зубцовых гармоник. |
Предположим, что ротор вращается со скоростью n, меньшей, чем скорость вращающегося потока основной гармоники п1. Тогда частота токов, индуктированных в роторе, будет пропорциональна разности
n1 — n.
С такой скоростью, равной n1 — n, будет перемещаться относительно ротора основная гармоника м. д. с., созданной токами ротора (эта 1-я гармоника на фиг. 102 не показана). Остановим наше внимание на какой-нибудь из гармоник ротора v-го порядка, имеющей в v раз больше полюсов и перемещающейся относительно
| ротора со скоростью | n1 — n | |
| v |
Как видно из фиг. 102, эта гармоника ротора В перемещается относительно проводовротора
| со скоростью | n1 — n | , а сам ротор перемещается в противоположную сторону со скоростью n; |
| v |
| n — | n1 — n | . |
| v |
При неподвижном двигателе (когда n = 0) гармоника В, как показывает вышеописанное выражение, будет вращаться в пространстве со скоростью n1/v. При синхронной скорости (т. е. когда п = n1) гармоника В в пространстве будет вращаться со скоростью, равной n1.
Отсюда видно, что гармоника В ротора вообще вращается в пространстве со скоростью, отличной от скорости гармоники А статора.
Однако есть число оборотов ротора n, при которых скорости кривых А и В в пространстве будут одинаковыми. Это условие математически может быть выражено следующим образом:
| n1 | = n - | n1 - n | . |
| v | v |
Из последнего уравнения найдем
| n = | 2n1 | = | n1 | = | n1 | , |
| 1 + v | (1 + v)/2 | k |
| k = | 1 + v | . |
| 2 |
Предположим для примера, что в кривой магнитного потока имеются гармоники порядка v = 7, 13 и 19. Подставляя эти значения в последнюю формулу, найдем для разных гармоник соответственно:
| k = | 1+ v | = | 1 + 7 | = 4 |
| 2 | 2 |
| k = | 1+ v | = | 1 + 13 | = 7 | ; |
| 2 | 2 |
| k = | 1 + 19 | = 10. |
| 2 |
Отсюда следует, что при достаточно резко выраженных зубцовых полях ротора для какого-нибудь двигателя возможно ожидать "застревания" ротора на следующих синхронных скоростях:
| n = | n1 | ; |
| 4 |
| n = | n1 | ; |
| 7 |
| n = | n1 | ; |
| 10 |
Отсюда видно, что 7-е гармоники статора и ротора "сцепляются" друг с другом при скорости n1/4 , 13-е гармоники "сцепляются" при скорости n1/7 и т. д.
Таким образом из этого рассмотрения явствует, что при известных условиях обычный асинхронный двигатель может представлять собой соединение в одно целое собственно асинхронной машины основной частоты и весьма большого числа синхронных и асинхронных машин, обтекаемых токами высших гармоник.
Попытаемся найти ответ на вопрос, какие условия способствуют в максимальной степени образованию "синхронного застревания"?
Выше было написано выражение для определения порядка высших гармоник в статоре:
| vzs = | z1 | ± 1 |
| p |
Для ротора можно написать такое же выражение
| vzr = | z2 | ± 1 |
| p |
Наилучшие условия для появления "синхронного застревания" получаются при совпадении порядка гармоник, т. е. когда
vzs = vzr,
z1/p±1 = z2/p ±1.
Из этого уравнения получаются следующие решения:
z2 — z1 = 2p;
z2 — z1 = — 2р.
Опасными являются не только те соотношения между числом зубцов в статоре и роторе, которые получаются из вышеописанных уравнений. Опыт показывает, что опасными являются также и соотношения, которые получаются из уравнения
x1z1 — x2z2 = ± 2p;
x1 = х2 = 1 или 2;
z1 — z2 = ± р.
Резюмируя все сказанное, еще раз напишем здесь соотношения, из которых получаются запретные числа пазов:
z2 — z1 = ±2p;
z2 — z1 = ±1p.
7. Форма кривых крутящих моментов. Выше было выяснено, что зубцовые гармоники могут вызвать паразитные крутящие моменты, которые при разбеге двигателя могут создать большие затруднения и могут вызвать значительные искажения кривой крутящих моментов от основной гармоники вращающегося поля.
1 Здесь х — целое число.
Выше было также выяснено, что следует различать "асинхронные" и "синхронные" паразитные моменты.
Для иллюстрации влияния "асинхронного" паразитного момента на фиг. 104 в виде примера показана кривая изменения крутящего момента при разных числах оборотов двигателя, имеющего в статоре катушечную обмотку с q = 2.
Для такой обмотки порядок зубцовой гармоники будет
vz = 2mq + 1 = 2 • 3 • 2 + 1 = 13.
Поэтому в такой машине можно ожидать в кривой крутящих моментов "провала" при скорости, равной
| 1500 | = 115,4 об/мин. |
| 13 |
 |
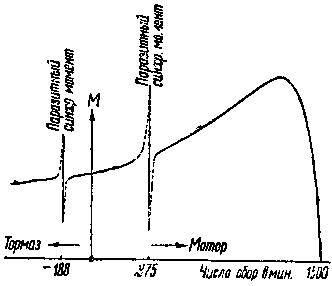 |
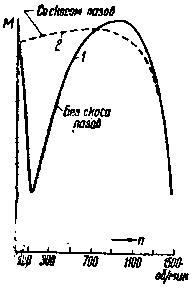
| Фиг. 103. Влияние скоса пазов на форму кривой крутящих моментов. | Фиг. 104. Паразитный синхронный момент. |
На опыте такой "провал" был действительно обнаружен, как показывает кривая 1 фиг. 103, снятая для одного экспериментального двигателя.
Если двигатель выполнить со скосом пазов в роторе, то вместо кривой 1 получится кривая 2, в которой "провал" уже будет отсутствовать.
Для иллюстрации влияния "синхронного" паразитного момента на форму кривой крутящих моментов на фиг. 104 показана кривая крутящих моментов, снятая для двигателя имеющего в статоре z1= 36 пазов и в роторе z2 = 16 пазов.
Как видно из этой фиг. 104, при моторном режиме благодаря "синхронному" паразитному моменту может произойти "застревание" ротора на скорости 375 об/мин (что соответствует 1/4 синхронной скорости при разгоне двигателя и пуске в ход). При тормозном режиме, как видно из фиг.104, такое же "застревание" ротора может произойти на постоянной скорости в 188 об/мин.
8. Шум в асинхронных машинах. При вращении ротора асинхронной машины, зубцы его перемещаются относительно неподвижных зубцов статора, вследствие чего в воздушном зазоре возникают пульсации магнитного потока.
Эти пульсации потока вызывают резкие периодические изменения величины магнитной индукции в зубцах статора и ротора.
Благодаря периодическому изменению объемных размеров зубцов, вызванному изменением магнитной индукции в зубцах (магнитострикционные явления), может возникнуть шум, гудение или "пение" асинхронных двигателей.
Этот шум, главным образом, вызывается чрезмерным магнитным насыщением зубцов двигателей и может быть ослаблен при уменьшении магнитного насыщения.
Шум может быть также вызван радиальной и тангенциальной вибрацией зубцов статора и ротора.
В особенности резкие тангенциальные колебания зубцов возникают при появлении "синхронных" моментов, вызванных зубцовыми гармониками, о чем говорилось выше.
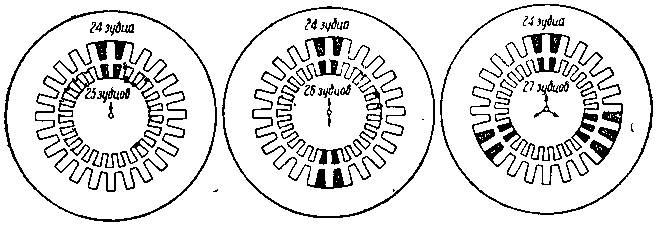 |
| Фиг. 105. Чертеж, поясняющий причину возникновения шума в двигателях. |
Поэтому следует при проектировании машины избегать таких соотношений между числом зубцов статора z1 и ротора z2, при которых получается z1 = z2 или z1— z2 = ± 2р, или z1— z2 = ± р.
Есть еще другая причина шума:
Радиальные силы, вызывающие одностороннее притяжение ротора к статору, могут послужить причиной сильных вибраций ротора и шума двигателя.
О существовании односторонних радиальных сил притяжения, действующих на ротор, можно получить представление на основании фиг. 105, где слева изображен статор с числом зубцов z1 = 24 и ротор с z2 = 25.
При условиях этой фигуры для данного положения зубцов ротора относительно зубцов статора появится наибольшая сила притяжения между двумя зубцами статора и ротора с совпадающими осями (заштрихованными на фиг. 105).
Вследствие этого возникает одностороннее радиальное притяжение ротора к статору.
При вращении ротора направление этой радиальной силы будет также изменяться, что вызовет механические вибрации всего тела ротора и как следствие — шум машины.
Если скорость вращения в пространстве радиальной силы такова, что она попадает в резонанс с собственными упругими колебаниями вала ротора, могут возникнуть настолько сильные вибрации ротора, что последний начнет задевать железо статора, что сделает работу двигателя невозможной.
Поэтому при проектировании асинхронных двигателей с короткозамкнутым ротором следует избегать таких чисел зубцов в роторе, при которых получается z2— z1= ± 1.
Однако с точки зрения возможности вибрации ротора и шума являются также опасными и другие сооружения зубцов статора и ротора, при которых получатся z1— z2 = ± 2, или z1— z2 = ± 3.
Как видно из среднего рисунка фиг. 105 при z1— z2= ± 2 возникают в зазоре две зоны радиальных сил (соответственные зубцы для наглядности заштрихованы).
При z1— z2= ± 3появляется три зоны радиальных сил (см. правый чертеж на фиг. 105).
Возникающие при неблагоприятном сочетании зубцов статора и ротора радиальные силы подвергают периодической деформации не только железо ротора, но и железо статора двигателя, причем особенно сильными эти деформации получаются при z1— z2= ± 1 или z1— z2= ± 2.
Как показывает детальное изучение этого вопроса, 1 во избежание шума следует избегать следующих соотношений между числами зубцов статора и ротора:
z2— z1= ±2p—+2;
z2— z1= ±2p—+3;
z2— z1= ±2p—+4.
Опыт показывает, что двигатели "шумят" также в том случае, когда в статоре обмотка выполнена с дробным числом пазов на полюс и фазу (т. е. когда имеется q1 = 21/2, 31/2, 41/2 и т. д.) или когда беличья обмотка ротора имеет нечетное число проводов z2.
Поэтому при проектировании двигателя следует брать в короткозамкнутом роторе z2 — четное, а также избегать в статоре дробных значений q1.
9. Общие замечания относительно выбора числа пазов в короткозамкнутом роторе. а) Вследствие влияния зубцовых потоков, как было выяснено выше, возможно "застревание" ротора на скорости, равной
| n1 | . |
| z1/p + 1 |
Это "застревание" исчезает при z2 = z1 + p и достигает максимального значения при z2 = 2z1.
Поэтому следует избегать двойного (или близкого к нему) числа пазов в роторе по сравнению со статором.
1 См. проф. Б. П. А п а р о в, Машины переменного тока. т. I, стр. 224; R. Richter "Elektrische Maschinen", т. IV, стр. 206; Möller, "Archiv für Elektro-technik", Bd. 24 (1930), S. 401, 900.
б) Следует избегать в короткозамкнутом роторе нечетного числа пазов z2, при котором часто наблюдается "гудение" двигателя, вызванное несимметричностью результирующей зубцовых полей статора и ротора 1.
в) Точно так же следует избегать всякой несимметричности
в обмотке статора (таким образом по возможности следует избегать катушечной обмотки с дробным числом пазов на полюс и фазу).
г) Скверный разбег двигателя получается при числе пазов в роторе, отличающемся от числа пазов статора на 2р,т. е. когда z1— z2 = ± 2р.
Как показывает опыт, при таких соотношениях зубцов двигатель не разбегается до нормальной скорости и "застревает" на низкой скорости, причем благодаря своеобразному взаимодействию между зубцовыми потоками ротор вращается при этом с синхронно-постоянной
| скоростью, равной | n1 | . |
| z2/2р |
Если z2 < z1, такое "синхронное застревание" ротора происходит при отрицательном асинхронизме (Möller, "A. f. Е.", 1930, S. 401).
Такое же "синхронное застревание" возможно и при других соотношениях числа зубцов статора и ротора, когда
z1 — z2 = ± р или z1 — z2 = ± 4р.
Поэтому рекомендуется таких соотношений числа зубцов статора и ротора избегать.
д) Как показывают исследования Fritze, Dreyfus'a и Stiel'а, нежелательными являются также соотношения зубцов
х(z1 — z2) = ± 2р ± 1,
z1 — z2 = ± 4р ± 2
z1 — z2 = ± 2p ± 1.
При несоблюдении вышеприведенных условий может появиться в двигателе весьма опасное явление одноосного притяжения ротора и вибрации, затрудняющих разбег двигателя 2.
е) В роторе Бушеро 3 благодаря увеличенному сопротивлению наружной клетки влияние зубцовых потоков оказывается менее заметно.
1 См. статью Б. П. Апарова, "Электричество", 1921, стр. 73; Fritze "A. f. E." В. 10, 1921, S. 73; Punga und Raydt, "Drehstrommotoren mit Doppelköfigauker". J. Springer, 1931.
2 Изучение вопроса о влиянии зубцовых потоков на работу двигателя приводит к весьма сложным теоретическим выкладкам. Желающим изучить этот вопрос можно рекомендовать работу Б. А. Апарова, Теория искаженной кривой крутящих моментов, "Электричество" № 8, 1932.
На иностранных языках можно рекомендовать следующую литературу: Stiel, Vorschungsarbeiten, bd. 5 „VDI" № 212; Wandenberg, Wissenschaftliche veröffentlichungen aus dem Simens-Konzern, B. 24, № 3; Dreese, „Am. I. E. E.",1930.
3 См. ниже гл. XVI.
ж) Радикальный метод борьбы с зубцовыми потоками кроме надлежащего выбора числа пазов в роторе z2 заключается также в скосе паза ротора, равном зубцовому делению статора. Увеличение воздушного зазора также несколько ослабляет влияние зубцовых полей.
Скос пазов в роторе улучшает при известных условиях пусковые свойства двигателей.
Однако чрезмерный скос пазов служит причиной увеличения реактанца магнитного рассеяния и потому ухудшает коэфициент мощности двигателя.
Поэтому при проектировании асинхронных двигателей путем выбора правильного сочетания числа пазов статора и ротора необходимо стремиться к тому, чтобы скос пазов ротора являлся излишним.
По Дрейфусу рекомендуется делать скоспаза в роторе на радиальный угол
| α = | 2π | . |
| z1+ p |
При этих условиях сводится на-нет влияние весьма опасной гармоники порядка
| k = | z1 | ± 1. |
| p |
з) Учитывая все вышеприведенные требования, касающиеся пусковых характеристик двигателя, можно составить следующие таблицы для выбора числа пазов в короткозамкнутом роторе z2 при известном числе пазов в статоре z1 для различных чисел полюсов 2р 1.
На основании более поздних данных (по Рихтеру2) можно выбирать число пазов в роторе в более широких пределах, руководствуясь следующей таблицей:
ТАБЛИЦА 12
| р | z1 | z2 | p | z1 | z2 | p | z1 | z2 |
| 2 | 24 36 48 |
18, 30, 34, 38 10, 14, 22, 26, 30, 42, 46, 50, 54, 58 10, 14, 18, 30, 34, 38, 42, 54, 58, 62, 66 |
3 | 36 54 |
10, 14, 16, 20, 22, 26, 27, 28, 32, 34, 38, 40, 44, 45, 46, 50, 51, 52, 56, 57, 58 10, 14, 15, 16, 20, 21, 22, 26, 28, 32, 33, 34, 38, 39, 40, 44, 45, 46, 50, 52, 56, 58, 62, 63, 64, 68, 69, 70, 74, 75, 76 |
6 | 72 | 10, 14, 15, 16, 20, 21, 22, 26, 27, 28, 32, 34, 38, 40, 44, 45, 46, 50, 51, 52, 56, 57, 58, 62, 63, 64, 68, 70, 74, 76, 80, 81, 82, 86, 87, 88, 92, 93, 94, 98, 99 |
На основании опытов Меллера3 выяснилось, что нечетные числа пазов в роторе z2 за редкими исключениями вызывают шум мотора (в особенности при пуске и разгоне мотора) и что такого шума обычно не наблюдается в случае четного числа пазов в роторе.
1 См. "Е. u. М." № 31, 1932, Sequenz, Die Wahl der Nutenzahlen bei Käfigankermotoren.
2 Richter, Elektrische Maschinen, B. IV, стр. 211.
3 Archiv für Elektrotechnik, 1930, стр. 401 и 900.
Поэтому предпочтительно выбирают в роторе по мере возможности четное число пазов.
