§ 193. Сопротивления клеток ротора Бушеро

[an error occurred while processing this directive]

Все справочники Предисловие

Введение

Введение

§ 1. Краткий исторический обзор § 2. Опыт Фарадея § 3. Принцип действия современного асинхронного двигателя § 4. Вращающееся магнитное поле (двухфазное) § 5. Вращающееся магнитное поле, создаваемое трехфазным током

Глава I

Глава I. Обмотки асинхронных двигателей

§ 6. Классификация § 7. Катушечные обмотки § 8. Связь между числом полюсов и числом шпуль катушечной обмотки § 9. Катушечная обмотка при нечетном числе пар полюсов (р) § 10. Катушечная обмотка с дробным числом пазов на полюс и фазу (q) § 11. Схемы двухплоскостных и трехплоскостных катушечных обмоток § 12. Катушечная обмотка для разъемного статора § 13. Симметричная катушечная обмотка § 14. Катушечная обмотка с "короткими" шпулями § 15. Влияние укорочения шага обмотки на форму кривой индуктиро ванной э. д. с. § 16. Обмотки с укороченным шагом § 17. Трехфазная двухслойная обмотка (так называемая "американская") § 18. Фазная стержневая обмотка ротора § 19. Разрезные обмотки постоянного тока § 20. Способы намотки § 21. Открытые пазы § 22. Открытые и полузакрытые пазы § 23. Американская и европейская системы изоляции обмоток § 24. Изоляция паза

Глава II

Глава II. Роторные обмотки

§ 25. Классификация § 26. Беличье колесо § 27. Роторная обмотка с короткозамкнутыми секциями § 28. "Комбинированные" роторные обмотки

Глава III

Глава III. Обмоточный коэфициент

§ 29. Понятие об обмоточном коэфициенте § 30. Общее выражение для наведенной э. д. с § 31. Влияние характера размещения обмотки в пазах на величину обмоточного коэфициента "распределения" § 32. Общая формула для нахождения величины обмоточного коэфициента „распределения"kp § 33. Обмоточный коэфициент „распределения" гладкой обмотки § 34. Обмоточный коэфициент „распределения" многофазной обмотки § 35. Обмоточные коэфициенты высших гармоник

Глава IV

Глава IV. М. д. с. обмоток асинхронного двигателя

§ 36. Кривая м. д. с. однофазной обмотки § 37. Разложение в ряд Фурье кривой м. д. с. § 38. Общее выражение для нахождения величин м. д. с. в любой момент времени (t) и в любой точке (х) окружности статора § 39. Кривая м. д. с. для трехфазной обмотки § 40. Уравнение м. д. с. вращающегося поля для трехфазной обмотки § 41. М. д. с, создаваемая обмотками с большим числом пазов на полюс и фазу (q) § 42. М. д. с. равномерно распределенной трехфазной обмотки § 43. Многоугольник Гергеса

Глава V

Глава V. Э. д. с, индуктированные в обмотках асинхронного двигателя

§ 44. Магнитные потоки в асинхронном двигателе. § 45. Э. д. с, индуктированные потоками рассеяния ФS1 и ФS2 § 46. Э. д. с, наводимые потоком Ф

Глава VI

Глава VI. Асинхронный двигатель как трансформатор

§ 47. Ток ротора § 48. Изменение величины магнитного потока Ф. § 49. Величина потока Ф § 50. Связь между ампервитками статора (AW1) и ротора (AW2) § 51. Диаграмма ампервитков § 52. Диаграмма токов § 53. Коэфициент трансформации § 54. "Приведенные" величины § 55. Аналогия между асинхронным двигателем и трансформатором § 56. Векторная диаграмма неподвижного двигателя

Глава VII

Глава VII. Явления, происходящие во вращающемся двигателе

§ 57. Общее выражение крутящего момента § 58. Диаграмма ампервитков и токов вращающегося двигателя § 59. Скольжение и частота в роторе § 60. Зависимость между скольжением и э. д. с. фазного ротора § 61. Ток фазного ротора в функции скольжения двигателя § 62. Эквивалентная схема для роторного тока § 63. Два вида векторной диаграммы э. д. с. и тока ротора § 64. Полная векторная диаграмма вращающегося двигателя § 65. Векторная диаграмма э. д. с. и потоков

Глава VIII

Глава VIII. Ротор в виде беличьей обмотки (короткозамкнутый ротор)

§ 66. Надежность беличьего ротора § 67. Электродвижущие силы и токи в беличьей обмотке ротора

Глава IX

Глава IX. Асинхронный двигатель как универсальный преобразователь

§ 68. Асинхронный двигатель как универсальный преобразователь § 69. „Энергетическая" диаграмма § 70. Мощность, подводимая к ротору вращающимся магнитным потоком (PS) § 71. Механическая аналогия

Глава X

Глава X. Крутящий момент

§ 72. Полное выражение крутящего момента § 73. Величина крутящего момента, выраженная в „синхронных ваттах" (PS) § 74. Связь между величиной крутящего момента и джоулевыми потерями в обмотке ротора § 75. Пусковой момент § 76. Зависимость величины крутящего момента от величины магнитного потока § 77. Влияние напряжения U на величину крутящего момента § 78. Максимальная величина крутящего момента § 79. Влияние величины активного сопротивления цепи ротора на величину пускового момента § 80. Форма кривой крутящего момента § 81. Связь между Mmax , M и скольжением s § 82. Крутящий момент при малых скольжениях § 83. Зависимость крутящего момента от частоты f1тока, питающего двигатель, и омического сопротивления цепи ротора r2 § 84. Кривая начального момента вращения в функции сопротивления цепи ротора § 85. „Гистерезисный" момент § 86. Местные магнитные потоки и явления „прилипания" § 87. Мощность ротора (Р'2) и скольжение (s) § 88. Зубцовые поля и влияние их на форму кривой крутящего момента и на шум машины

§ 89. Влияние скоса пазов ротора на высшие гармоники

Глава XI

Глава XI. Потери и к. п. д.

§ 90. Потери в асинхронном двигателе § 91. Потери холостого хода § 92. Перемагничивание железного цилиндра, вращающегося в постоянном магнитном поле § 93. Перемагничивание железного ротора вращающимся потоком § 94. Потери на гистерезис в статоре асинхронного двигателя § 95. Формула для подсчета потерь на гистерезис § 96. Вихревые токи, появляющиеся в железе ротора при его вращении § 97. Потери на токи Фуко в железе статора § 98. Формулы для подсчета потерь на токи Фуко § 99. Формула для подсчета суммарных потерь железа § 100. Потери на гистерезис и вихревые токи в сердечнике статора (индекс s) § 101. Потери на гистерезис и вихревые токи в зубцах статора (индекс z) § 102. Влияние механической обработки на потери в железе § 103. Потери в железе ротора § 104. Добавочные потери в железе § 105. Потери в болтах § 106. Учет дополнительных потерь § 107. Нагрузочные потери § 108. Вихревые потери в меди статора и ротора § 109. Экспериментальное исследование явления „вытеснения тока" (Опыты К. И. Шенфера и А. И. Москвитина) § 110. Форма кривых токов, текущих в проводах ротора §111. Механические потери § 112. Потери на трение в подшипниках § 113. Потери на трение щеток о контактные кольца § 114. Вентиляционные потери § 115. Коэфициент полезного действия § 116. Кривые к. п. д

Глава XII

Глава XII. Нагревание машин

§ 117. Влияние нагревания на продолжительность службы изоляции § 118. Изменение температуры нагрева электрической машины в функции времени § 119. Классификация изолирующих материалов § 120. Допускаемый нагрев машины § 121. Эмпирические формулы для подсчета перегрева машины § 122. Общее выражение для нахождения повышения температуры § 123. Повышение температуры железа статора § 124. Влияние вентиляционных прослоек на величину удельной поверхности охлаждения § 125. Нагрев меди статора § 126. Нагрев меди ротора § 127. Теплопроводность изолирующих и активных материалов § 128. Расчет вентилятора § 129. Машины „закрытого типа"

Глава XIII

Глава XIII. Вывод круговой диаграммы

§ 130. Опыт § 131. Краткая история § 132. Простейшая цепь, имеющая круговую диаграмму § 133. Другой вид векторной диаграммы асинхронного двигателя § 134. Эквивалентная схема для векторной диаграммы согласно фиг. 143 (левый чертеж) § 135. Упрощенная схема замещения § 136. Токи короткого замыкания I2k и I2ki § 137. Доказательство существования круговой диаграммы для полной схемы замещения § 138. Поправка на падение напряжения в статоре I0x1 § 139. Другой способ доказательства существования круговой диаграммы § 140. Опыт холостого хода и короткого замыкания § 141. Влияние магнитного насыщения на очертания „круговой диаграммы"

Глава XIV

Глава XIV. Пользование круговой диаграммой

§ 142. Джоулевы потери на круговой диаграмме § 143. Подводимая мощность (P1) § 144. Полезная мощность (Р2) § 145. Крутящий момент § 146. Физический смысл точки К∞ § 147. Физический смысл точки К § 148. Коэфициент мощности (cos φ) § 149. Скольжение § 150. Построение круговой диаграммы § 151. Максимальная величина коэфициента мощности

Глава XV

Глава XV. Асинхронная машина как генератор

§ 152. Асинхронная машина как генератор § 153. Параллельная работа асинхронного генератора с сетью § 154. Самовозбуждение асинхронного генератора § 155. Асинхронная машина как электротормоз (вращение "против поля")

Глава XVI

Глава XVI. Пуск в ход многофазных асинхронных двигателей
(при фазной обмотке ротора)

§ 156. Способ пускового реостата § 157. Крутящий момент при неподвижном двигателе § 158. Величина крутящего момента при вращении двигателя § 159. Пусковые реостаты § 160. Включение индуктивного сопротивления в цепь ротора § 161. Включение в цепь ротора реостата через посредство трансформатора (метод "третичных" токов Рюденберга) § 162. Метод дроссельной катушки с массивным железным сердечником § 163. Нестационарные процессы, происходящие в асинхронном двигателе в момент включения его обмоток на сеть § 164. Пусковые свойства двигателей с беличьим ротором

Глава XVII

Глава XVII. Пуск в ход многофазных асинхронных двигателей
(при короткозамкнутой обмотке ротора)

§ 165. Пуск в ход по методу пересоединения со звезды на треугольник § 166. Работа асинхронного двигателя при соединении его статора в звезду и треугольник § 167. Метод автотрансформатора § 168. Двигатель с двойным статором Бушеро § 169. Двигатель Брункена (Brunken) § 170. Двигатель с двойной беличьей клеткой ротора § 171. Кривая крутящего момента двигателя с двойной клеткой § 172. Алюминиевая обмотка ротора. Глубокие пазы § 173. Другие модификации ротора Бушеро § 174. Нагрев пусковой клетки § 175. Ротор в виде массивного железного цилиндра § 176. Пуск в ход больших асинхронных двигателей с короткозамкнутым ротором § 177. Двигатель Рихтера

Глава XVIII

Глава XVIII. Безреостатный пуск в ход асинхронных двигателей с фазным ротором по методу "противосоединения"

§ 178. Схемы Гергеса § 179. Токи ротора при второй схеме противосоединения (шестифазной) § 180. Величина коэфициента взаимоиндукции § 181. Коэфициент самоиндукции одной фазы ротора при его рабочем соединении § 182. Сдвиг фаз в роторе

Глава XIX

Глава XIX. Другие методы противосоединения. Короткозамкнутый двигатель как наиболее распространенный тип

§ 183. Описание схемы противосоединения, предложенной автором § 184. Переключение обмотки ротора в рабочее положение § 185. Пуск в ход по методу противосоединения обмоток статора(Б. П. Апарова) § 186. Коэфициент эффективности пуска § 187. Сопоставление трех типов двигателей с короткозамкнутым ротором § 188. Наиболее распространенный тип асинхронного двигателя с безреостатным пуском

Глава XX

Глава XX. Краткая теория ротора с двойной беличьей клеткой и с глубоким пазом

§ 189. Схема замещения для двигателя с двойной клеткой § 190. Токи в двойной клетке § 191. Отношение токов IА/IВ в функции скольжения § 192. Векторная диаграмма э. д. с. и токов в роторе Бушеро § 193. Сопротивления клеток ротора Бушеро § 194. Зависимость активного и реактивного сопротивления ротора Бушеро от скольжения § 195. Режим малых скольжений § 196. Режим больших скольжений § 197. Круги диаграммы тока двигателя с двойным беличьим ротором § 198. Полная диаграмма тока двигателя с двойным беличьим ротором § 199. Сопоставление свойств двигателей Бушеро и с глубоким пазом § 200. Двигатель с глубоким пазом

Глава XXI

Глава XXI. Однофазные асинхронные двигатели. Теория вращающихся в противоположные стороны полей

§ 201. Общие свойства § 202. „Прямое поле" и „инверсное" поле § 203. Крутящий момент однофазного двигателя § 204. Кривые тока в роторе однофазного асинхронного двигателя § 205. Два спаренных многофазных асинхронных двигателя, магнитные потоки которых вращаются в противоположные стороны § 206. Крутящий момент агрегата, описанного в предыдущем параграфе § 207. Кривые момента однофазного асинхронного двигателя

Глава XXII

Глава XXII. Однофазные асинхронные двигатели. Теория „поперечного" поля

§ 208. Потоки в статоре однофазного асинхронного двигателя при неподвижном и вращающемся роторе § 209. Эллиптическое вращающееся поле

Глава XXIII

Глава XXIII. Системы однофазных асинхронных двигателей

§ 210. Начальный момент однофазного двигателя § 211. Метод Корсепиуса (Korsepius) § 212. Двигатель Пунга (Punga) § 213. Схемы Тесла и Штейнметца (Tesla и Steinmetz) § 214. Конденсаторные асинхронные двигатели

Глава XXIV

Глава XXIV. Регулирование скорости асинхронных двигателей
по методу изменения числа оборотов в минуту вращающегося поля

§ 215. Скорость вращения магнитного потока § 216. Двигатель с двойной обмоткой в статоре § 217. Переключение обмотки на другое число полюсов § 218. Асинхронный двигатель с двойным ротором

Глава XXV

Глава XXV. Каскадное соединение двух асинхронных двигателей

§ 219. Регулирование скорости асинхронного двигателя путем включения в цепь ротора реостата § 220. Каскадное соединение двух асинхронных двигателей § 221. Скорость каскадного агрегата § 222. Распределение мощности между машинами каскадного агрегата § 223. Эквивалентная схема для каскадного соединения § 224. Ток холостого хода в статоре двигателя I § 225. Ток, текущий в статоре двигателя I при неподвижном агрегате § 226. Коэфициент мощности при каскадных схемах § 227. Явление Гергеса § 228. Явления, происходящие при каскадном соединении асинхронных двигателей с однофазным ротором § 229. Практическое значение схемы § 230. Каскадное соединение асинхронных двигателей с переключением числа полюсов § 231. Обзорная таблица каскадных схем § 232. Двухмоторная схема (для подъемников) § 233. Регулирование скорости по методу инверсного поля

Глава XXVI

Глава XXVI. Каскадное соединение асинхронных двигателей с коллекторными машинами

§ 234. Краткая история § 235. Краткий обзор схем соединения § 236. Каскадное соединение асинхронного двигателя с машинами постоянного тока § 237. Схема Кремера с шестифазным конвертором

а) Устойчивость работы схемы Кремера б) Схема Кремера с вольтодобавочной машиной

§ 238. Схема Шербиуса с машинами постоянного тока § 239. Различные виды каскадных соединений § 240. Каскадное соединение асинхронного двигателя с коллекторным при непосредственном механическом соединении (схема Кремера) § 241. Мощность каскадного агрегата по схеме Кремера § 242. Влияние характера возбуждения вспомогательного двигателя на работу агрегата § 243. Регулирование скорости при каскадном соединении асинхронного двигателя с шунтовым коллекторным двигателем § 244. Описание схемы Шербиуса § 245. Действие схемы § 246. „Энергетическая" диаграмма схемы Кремера § 247. „Энергетическая" диаграмма схемы Шербиуса § 248. Регулирование скорости ниже синхронной при схеме Шербиуса § 249. Сверхсинхронная скорость § 250. Переход через синхронизм § 251. Схема каскадного соединения, при которой возможен плавныйпереход главного двигателя через синхронную скорость

Глава XXVII

Глава XXVII. Компенсаторы сдвига фаз

§ 252. Компенсаторы сдвига фаз с самовозбуждением § 253. Компенсатор Шербиуса § 254. Работа компенсатора с самовозбуждением при разных нагрузках главного двигателя § 255. Компенсаторы шунтового возбуждения

Глава XXVIII

Глава XXVIII. Компенсированные асинхронные двигатели

§ 256. Двигатель Гейланда (Heyland) завода Бергмана (Bergmann)

Глава XXIX

Глава XXIX. Синхронно-индукционные двигатели

§ 257. Различные методы улучшения cosφв асинхронных двигателях § 258. Синхронно-индукционные двигатели § 259. Круговая диаграмма синхронного индукционного двигателя § 260. Различные способы соединения обмотки ротора с возбудителем § 261. Синхронно-индукционный двигатель с автоматическим регулированием cos φ § 262. Индукционная машина двойного питания

Глава XXX

Глава XXX. Нестационарные процессы, происходящие в асинхронном двигателе при переходных режимах

§ 263. Внезапное включение на сеть асинхронного двигателя при разомкнутом роторе § 264. Внезапное включение статора асинхронного двигателя на сеть при закороченном роторе § 265. „Бросок" тока при включении на сеть магнитно-насыщенного статора асинхронного двигателя § 266. Перенапряжения в обмотках асинхронных двигателей

Глава XXXI

Глава XXXI. Нормальные свойства асинхронных машин

§ 267. Нормальные свойства асинхронных машин § 268. Вес машины § 269. Серии асинхронных двигателей, построенных советскими заводами

Глава XXXII

Глава XXXII. Расчет асинхронного двигателя

§ 270. О математической неопределенности расчета электрических машин § 271. Расчетные варианты § 272. Главные размеры машины § 273. "Длинные" и "короткие" машины § 274. Расчетная длина ( li ) § 275. Коэфициент формы кривой поля ( αi ) § 276. Величина магнитного потока § 277. Основное уравнение § 278. Физический смысл постоянной С; удельное тяговое усилие § 279. Исследование основного уравнения § 280. Влияние Вl и AS на размеры машины § 281. Влияние числа оборотов в минуту n1 § 282. Машинная постоянная § 283. Влияние выбора плотности тока на размеры машины § 284. Связь между величиной полюсного деления и мощностью машины § 285. Влияние быстроходности, величины Вl и δ на ток холостого хода § 286. Выбор величины воздушного зазора (δ) § 287. Пример

Глава XXXIII

Глава XXXIII. Железо и обмотки статора и ротора

§ 288. Расчет обмотки статора § 289. Число пазов статора и объем тока § 290. Связь между объемом тока Iп и линейной нагрузкой AS § 291. Число пазов на полюс и фазу в статоре (q1) § 292. Ход расчета зубцов статора § 293. Ширина зубцов и пазов статора § 294. Очертание зубцов § 295. Выбор числа витков одной фазы w2 роторной обмотки § 296. Число пазов в роторе (Z2) § 297. Ток в фазе обмотки ротора § 298. Сечение проводов фазной обмотки ротора § 299. Расчет пазов и зубцов ротора § 300. Глубина паза hn § 301. Величина магнитного потока § 302. Определение высоты железного сердечника статора и ротора § 303. Ротор с беличьей обмоткой § 304. Размеры роторных контактных колец и щеток

Глава XXXIV

Глава XXXIV. Расчет магнитной цепи

§ 305. Величина тока холостого хода § 306. Участки магнитной цепи асинхронного двигателя § 307. Нахождение ампервитков для зубцов статора (АWzs) § 308. Ампервитки для зубцов ротора (АWzr) § 309. Ампервитки для воздушного зазора (АWl) § 310. Ампервитки в сердечнике статора и ротора §311. Суммарные ампервитки

Глава XXXV

Глава XXXV. Ток короткого замыкания

§ 312. Ток короткого замыкания § 313. Активное сопротивление обмотки статора § 314. Активное сопротивление фазной обмотки ротора § 315. Приведенная величина активного сопротивления фазной обмотки ротора § 316. Реактивное сопротивление обмотки статора и ротора § 317. Удельная магнитная проводимость паза § 318. Активное и реактивное сопротивления обмотки в виде беличьего колеса § 319. Приведенные значения активного и реактивного сопротивления обмотки ротора в виде беличьего колеса § 320. Другое выражение приведенного реактивного сопротивления беличьей обмотки

Глава XXXVI

Глава XXXVI. Магнитные потоки рассеяния

§ 321. Потоки рассеяния в разных частях секции § 322. Магнитная проводимость паза λп § 323. Удельная магнитная проводимость потока рассеяния между головками зубцов (λz) § 324. Удельная магнитная проводимость потока рассеяния лобовых частей обмотки (λs) § 325. Расчет рассеяния торцевых или лобовых частей обмоток § 326. Суммарная удельная проводимость (λ) § 327. Влияние укорочения шага в двухслойных ("американских") обмотках на величину λ § 328. Приведенный реактанц обмотки ротора в виде беличьего колеса

Глава XXXVII

Глава XXXVII. Конструкция асинхронных машин

§ 329. Общий вид § 330. Конструкция ротора § 331. Приспособление для короткого замыкания § 332. Асинхронный двигатель сварной конструкции § 333. Двигатель с независимой вентиляцией § 334. Двигатель для центрифуги § 335. Новый тип двигателя для работы под водой § 336. Системы вентиляции § 337. Ротор с увеличенным активным сопротивлением § 338. Асинхронные двигатели производства советских заводов § 339. Двигатели типа Бушеро и с глубоким пазом производства советских заводов § 340. Некоторые технические данные, касающиеся асинхронных двигателей советского производства

Глава XXXVIII

Глава XXXVIII. Примерные расчеты

§ 341. Задание § 342. Задание

Обозначения

Оглавление

ГЛАВА XX
КРАТКАЯ ТЕОРИЯ РОТОРА С ДВОЙНОЙ БЕЛИЧЬЕЙ КЛЕТКОЙ И С ГЛУБОКИМ ПАЗОМ

§ 193. Сопротивления клеток ротора Бушеро.

Для удобства вывода формул будем исходить из схемы замещения для роторной цепи на фиг. 211, которая может быть получена из схемы замещения фиг. 208 путем помножения значений активных и реактивных сопротивлений на s.


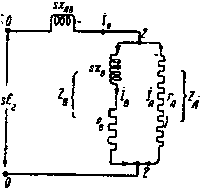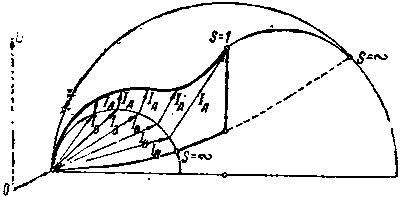
Фиг. 210. Диаграмма токов в роторе Бушеро.	Фиг. 211. Схема замещения для ротора Бушеро.

Желая получить решение задачи в общем виде, обозначим полные (кажущиеся) сопротивления параллельных ветвей между точками 2—2 схема через ZA и ZB 1.

1 В дальнейшем большими буквами будем обозначать кажущиеся сопротивления в комплексной форме.

Результирующее сопротивление цепи 2—2 будет

Z2 =	ZAZB	.
	ZA+ ZB

Подставляя в это выражение

ZA = rА,

ZB = rB + jsxB,

найдем

Z2 =	rA(rB+ jsxB)	.
	(rА + rB) + jsxB

Желая освободиться от мнимостей в знаменателе, помножим и числителя и знаменателя этого выражения на (rА + rB)— jsxB, после чего получим

Z2 =	rA(rB+ jsxB)[(rА + rB)— jsxB]	.
	(rА + rB)2 + s2xB2

или

Z2 =	rArB(rА + rB)+ s2xB2rА	+ j	sxBr2А	.
	(rА + rB)2 + s2xB2		(rА + rB)2 + s2xB2

Это комплексное выражение, состоящее из действительной и мнимой части, имеет вид

Z2 = r2f + jsx2f ,

где

(193.1)

r2f=	rB(rА+ rB) + s2xB2	rА,
	(rА+ rB)2 + s2xB2

(193.2)

x2f =	r2АxB	rА,
	(rА+ rB)2 + s2xB2

Оглавление

[an error occurred while processing this directive]