АСИНХРОННЫЕ
МАШИНЫ

ПРИМЕР РАСЧЕТА ТРЕХФАЗНОГО АСИНХРОННОГО ДВИГАТЕЛЯ С ГЛУБОКИМИ ПАЗАМИ В РОТОРЕ

§ 342. Задание.

Необходимо спроектировать асинхронный двигатель с короткозамкнутым ротором на 15 kW, 750 об/мин (синхр.), 220/380 V 50 герц. Для получения высокого пускового момента вращения ротор двигателя в виде беличьей клетки должен быть выполнен с глубокими пазами. Потери и перегрев должны удовлетворять условиям ОСТ.

I. Главные размеры

1) Число пар полюсов находим по формуле

р =	60f	=	60 • 50	= 4
	п		750

2) Согласно OCT 678 принимаем

3) Кажущаяся подведенная мощность в kVA будет

kVA =	kW	=	15	= 21.
	η cos φ		0,86 • 0,83

4) Предполагая статор соединенным в Y, найдем фазный ток в статоре

Il =	kVA 1 000	=	21 • 1 000	= 32 A.
	√3U		√3 • 380

5) Мощность на 1 полюс

kVA	=	21	= 2,62.
2p		8

6) По кривым находим для машины данной мощности величину машинной постоянной

Задаемся   предварительно  величинами Bl = 7 200 и AS = 330. Найдем для разных вариантов диаметр D и длину li машины. Ниже приводятся данные выбранного варианта:

ТАБЛИЦА 44

D cm	τ cm	AS	Bl	D2li	li cm	l1	ns х bs	liτ
26	10,2	330	7 200	9 440	13,9	14,9	l x l	1,36

7) Окончательно принимаем:

Число железных пакетов 2.

Длина железного пакета 7 cm.

Длина железа l = 2 • 7 = 14 cm.

Число вентиляционных каналов ns = 1.

Ширина вентиляционных каналов bs = 1.

Общая длина железа

Расчетная длина

8) Воздушный зазор согласно ОСТ 678 возьмем

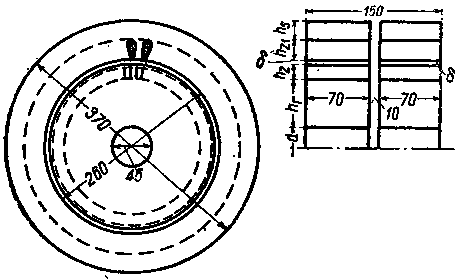Фиг. 386.

II. Обмотка, пазы, ярмо статора

9)   Число пазов на полюс и фазу выбираем   из  такого расчета, чтобы ширина   паза bn получилась   в   допустимых   пределах   (в   среднем от 0,6 cm до 1,3 cm).

Выбираем q= 2.

10)   Число пазов статора

11)     Зубцовое деление статора

ts =	nD	=	n • 260	= 17 mm.
	z1		48

12)  Принимаем для статора двухслойную американскую обмотку. Находим число проводов в пазу

sn =	t1AS	=	1,7 • 330	= 17,5.
	I1		32

13) Округляя, принимаем окончательно

14) Число витков в фазе статора

w1 =	snpq	=	18 • 4 • 2	= 144.
	a		1

15) Выбираем   для   статорной   обмотки   укороченный шаг  у ≈ 0,8t. Таким
образом шаг обмотки по пазам будет

Округляя до целого числа, получаем окончательно

16) Шаг в долях полюсного деления

β =	y	=	5	=	5	.
	3q		3•2		6

17) Обмоточный коэфициент распределения

	sin	π		sin	180
kр =		2m	=		2 • 3	=	sin 30°	= 0, 963.
	q1sin	π		2 sin	180		2 sin 15°
		2mq			2•3•2

18) Коэфициент укорочения шага

kу = sin (β • 90°) = sin	5	90° sin 75° = 0,966.
	6

19) Результирующий обмоточный коэфициент

20) Выбираем плотность тока статора

21) Сечение проводов статора

qa1 =	I1	=	32	7,1 mm2.
	Δ1		4.5

Согласно OCT 4123 выбираем медь с диаметром 3,05/3,35 и сечением

22) Чертим эскиз паза. По чертежу подсчитываем сечение паза θ = 318 mm2 (см. фиг. 387).

Коэфициент заполнения паза

qa1 • sn	=	7,3 •18	= 0,413,
θ		318

т. е. 41,3%.

23)   Принимаем класс изоляции А. Проводники — с изоляцией ПБД. Пазовая изоляция "латероид" толщиной 2 • 0,5 mm. Прокладка между верхним и нижним слоями (между секциями) — промасленное полотно толщиной 2 • 0,5 mm.

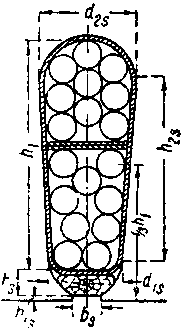Фиг.387

Деревянный клин.

24)   Проверяем нагрев обмотки.

а)   Длина лобовой части

б) Длина полувитка

в) Активное сопротивление фазы, приведенное к 75° С:

r1 = 1,24	2w1lа1	= 1,24	2 • 144 • 30,3.	= 0,264 Ω.
	5 700 qа1		5 700 • 7,3

г) Нагрев обмотки

Δt° =	55 (1,05mr1I12 + VFe )	.
	(1 + 0,1ns ) A

Подставляя в эту формулу значение найденного ниже
VFe = 340 и значение А (взятое по кривым 1 для диаметра D = 26), равное А = 1 700, найдем

Δt° =	55 (1,05 • 3 • 0,264 • 322 +340)	= 34,7° С..
	(1 + 0,1 • 1) 1700

25) Найдем магнитный поток при холостом ходе

Ф =	U • 108	=	220 • 108.	= 0,74 • 106.
	4,44k1w1f		4,44 • 0,93 • 144 • 50

26) При таком потоке максимальная индукция в воздушном зазоре получается

Bl =	Ф	=	0,74 • 106	= 7 250.
	aiτli		0,69 • 10,2 • 14,5

27) Наименьшая ширина зубца статора:

Индукция в зубцах

Bz max =	Blt1	=	7 250 • 1,7	= 17 000.
	z1min k2		0,8 • 0,91

Здесь k2 = 0,91 учитывает изоляцию   прослоек   при   бумажной   изоляции железных листов.

28) Найдем высоту ярма статора, задаваясь Bs = 13 200. Получим

hs =	Ф	=	0,74 • 106	= 2,2 cm.
	2k2lBs		2 • 0,91 • 14 • 13

Внешний диаметр статора

---

1 По В. А. Трапезникову "Основы проектирования серий асинхронных машин".

---

III. Обмотка, пазы и ярмо ротора

Ротор выполняем   короткозамкнутым   в форме беличьего колеса   с   "глубокими пазами".

29)  Число пазов ротора выбираем

30)  Ток в стержне ротора

Is =	Р • 1 000	,
	z2E2 • 0,93

где

E2 =	U	=	220	= 0,82 V,
	2w1k1		2 • 144 • 0,93

Is =	15 • 1 000	= 333 A.
	59 • 0,82 • 0,93

31) Принимаем сечение меди ротора

Плотность тока будет

s2 =	Is	=	333	= 6,65 A/mm2.
	qа2		50

Размеры паза ротора будут (см. фиг. 388).

32) Определяем ток в замыкающем кольце

Iк =

Is

=

333

=

333

=

333

= 792 A.

2 sin

p

180°

2 sin

4

180°

2 sin 12,2°

2 • 0,21

z2

59

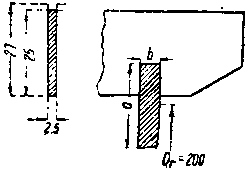Фиг. 388.

33) Сечение кольца примем

Плотность тока в кольце будет

sк =	Iк	=	792	= 5,3 A/mm2.
	qк		150

34) Зубцовое деление ротора

tr =	πDr	=	3,14 (260 — 2 • 0,5)	= 13,9 mm.
	z2		59

35) Находим диаметр вала

d = 14,4 • 3	√	л. с.	= 14,4  3	√	15 • 1,36	≈ 45 mm.
		n			750

36) Определяем высоту "спинки" ротора

IV. Расчет магнитной цепи

37) Индукция в зубцах статора

По чертежу:

Наибольшая ширина зубца

Средняя ширина зубца

Bz min =	Bl t1	=	7 250 • 1,7	= 14 600,
	k2 • zmax		0,91 • 0,93

Bz cp =	Bl t1	=	7 250 • 1,7	= 15 500.
	k2 • zср		0,91 • 0,865

38) Находим ампервитки для зубцов статора. кривой намагничивания находим:

Средние удельные ампервитки

awzs =	80 + 23 + 4 • 35	= 40,5.
	6

Суммарные зубцовые ампервитки

39) Точно так же найдем для зубцов ротора awzr = 8,8

40) Ампервитки для воздушного зазора

k0 = (	ts + 10δ	)(	tr + 10δ	)= 1,37,
	zs + 10δ		zr + 10δ

41) Находим ампервитки в железе статора. о кривой   намагничивания дли Bs = 13 200 найдем aws = 14.

42) Ампервитки железа ротора

Br =	Ф	=	0,74 • 106	= 3 640.
	2hrkrl		2 • 8 • 0,91 • 14

По кривой намагничивании   находим awr = 1, AWr = awr Lr = 1 • 3,5 = 3,5

43) Суммарные ампервтки на полюс

Найдем отношение

AW0	=	656	= 1,64.
AWl		400

44) Намагничивающий ток

Ior =	2,22 • AW0 • p	=	2,22• 656• 4	= 14,5 A.
	m • w1• k1		3 • 144• 0,93

45) Процентное значение намагничивающего тока

Ior% =	Ioб	100 =	14,5	100 = 45,5%.
	I		32

V. Параметры двигателя

46) Реактивное сопротивление рассеяния статорной обмотки.

x1 =	4πf1w12	λ • li ,
	p • q1• 108

где

а) Магнитная проводимость паза статора

λn = 1,25 • kn (	h1	+	h2	+	2h2	+	h1s	);
	3bn		bn		d1s + bs		bs

kn =	3β + 1	=	3 • 0,833 + 1	= 0,875,
	4		4

b) Магнитная проводимость для потоков   рассеяния   лобовых   соединений (двухслойная обмотка с сокращенным шагом)

λs = 0,4	τq	= 0,4	10,2 • 2	= 0,54.
	li		15

с) Магнитная проводимость между коронками зубцов

λz =	tr	=	13,9	= 1,74.
	18δ		18 • 0,5

d) Cуммарная магнитная  проводимость

e) Реактивное сопротивление фазы статора

x1 =	4π • 50 • 1442	4,06 • 14,5 = 0,95 Ω.
	4 • 2 • 108

17) Активное сопротивление фазы статора

r1 = k •	2w1la1 (1 + 0,004T)	= 0,264 Ω..
	5 700qa1

48) Активное и реактивное сопротивление   ротора

а)

r'2 = [rs +	2rr			]	4m1(w1k1)2	;
	(2sin	πp	)2		z2
		z2

Активное сопротивление стержня

rs = l	ρ	= 15,5	1	. 1
	100 • qa		46 • 100 • 50

rs =	15,5 • 1	= 6,73 • 10-5Ω
	46 • 100 • 50

(здесь 1/46 — удельное   сопротивление меди).

---

1 Здесь l — длина стержня.

---

b) активное сопротивление части замыкающего кольца между стержнями ротора

rr =	πDr ρ	= 15,5	π • 200 • 0,0218	= 0,155 • 10-5 Ω
	z2 • 100 • q		59 • 100 • 156

с)

r2 = rs +	2rr			= rs + Rr = 6,73 • 10-5 +	2 • 0,155 • 10-5			=
	(2sin	πр	)2		(2sin	180 • 4	)2
		z2				59

d) Приведенное активное сопротивление ротора

r'2 = r2•	4m1 (w1k1)2	= 8,49 • 10-5 •	4 • 3 (144 • 0,93)2	= 0,312 Ω.
	z2		59

е) Найдем приведенное реактивное сопротивление ротора. Для этой цели сначала подсчитаем удельную магнитную проводимость паза ротора (открытого)

λn2 = 1,25(	h1	+	h2	) = 1,25 (	25	+	2	) = 5,17.
	3bn		bn		3 • 2,5		2.5

f) Удельная магнитная проводимость головок зубцов ротора

λzr =	ts	=	17	= 2,13.
	18δ		18 • 0,5

g) Удельная проводимость торцевых колец ротора

λzr = 2,5	Dr	= 2,5	20	= 0,55.
	z2li		59 • 15,5

h) Суммарная магнитная проводимость

i) Реактивное сопротивление ротора, приведенное к статорной цепи,

х'2 = 377	(w1k1)2	liλ2 • 10-7,
	z2

х'2 = 377	(144 • 0,93)2	14,5 • 7,85 • 10-7 = 1,3 Ω.
	59

49) Найдем данные короткого замыкания, которые   получились   бы,   если бы, не было явления "вытеснения" тока.

cos φk =	rk	=	0,576	= 0,252;
	zk		2,28

Ik =	U	=	220	= 96,5 A;
	zk		2,28

Ik	=	96,5	= 3,02.
I1		32

VI. "Вытеснение" тока в стержне ротора

50) При пуске в ход активное и реактивное сопротивления   стержня   беличьей клетки могут быть выражены

Коэфициенты, входящие в эти выражения, могут быть найдены из следующих выражений:

kr = α •	sin h 2α + sin 2α	;
	cos h 2α — cos 2α

kх =	3	α•	sin h 2α + sin 2α	;
	2		cos h 2α — cos 2α

Здесь

Если   стержни   в   роторе медные высотой h, не превосходящей 5 cm, вышенаписанные выражения для kr и kх упрощаются и получают вид

kr = α = h √s; kx =	3	=	1,5	; kr = h; kx =	1.5	.
	2α		h √s		h

Подставляя сюда h = 2,5 cm, найдем

kr = 2,5; kx =	1,5	=0,6.
	2,5

Подсчитаем изменение (уменьшение  магнитной проводимости паза ротора при пуске

Найдем полную магнитную проводимость рассеяния ротора при пуске

Реактивное сопротивление ротора при пуске:

x'2k = x'2	λ'2	= 1,3	5,78	= 0,95 Ω.
	λ2		7,85

Общее реактивное сопротивление при пуске:

51) Найдем пусковое общее сопротивление двигателя с учетом влияния вытеснения тока

a) Как было найдено выше, активное сопротивление фазы беличьего ротора без учета влияния "вытеснения" равно

b) Активное сопротивление фалы с учетом вытеснения

c) Коэфициент увеличения активного сопротивления ротора

18,6 • 10-5	= 2,2. 1
8,49 • 10-5

---

1 Получилась величина, меньшая 2,5, вследствие влияния активного сопротивления торцевых частей беличьей клетки, в которых "вытеснение" тока невелико.

---

d) Приведенное активное сопротивление ротора с учетом „вытеснения"

r'2k = r'2(	r2k	) = 0,312 • 2,2 = 0,68 Ω.
	r2

e) Пусковое суммарное активное сопротивление

f) Пусковое общее сопротивление (с учетом "вытеснения")

g)

cos φk =	rk	=	0,944	= 0,45.
	zk		2,12

Таким образом видно, что "вытеснение" тока в стержнях ротора повышает коэфициент

мощности при пуске в отношении	0,45	.
	0,252

52) Пусковые характеристики двигателя

а) Пусковой ток с учетом вытеснения;

Ik =	U	=	220	= 104 A.
	zk		2,12

b) Кратность пускового тока

Ik	=	104	= 3,24,
I		32

с) Пусковой момент

Mk = m1Ik2 r'2k(	0,975	);
	ns

Mk = 3 • 1042 • 0,68 (	0,975	) = 28,6 kgm.
	750

Если бы в двигателе   отсутствовало   явление   "вытеснения"   тока,   то   мы получили бы

Mk = m1Ik2 r'2(	0,975	) = 3 • 96,52 • 0,312 (	0,975	) = 11,3 kgm.
	ns		750

VII. Коэфициент полезного действия двигателя

53)  Находим потери при номинальной нагрузке

Потери меди статора  V1 = 890 W

Потери меди ротора  V2 = 585 W "Добавочные" потери согласно   нормам   принимаем   равными   0,5% or подведенной мощности V0 = 0,005 Р1 = 0,005 • 17,3 = 86 W.

Механические потери принимаем равными 3% от полезной мощности

Потери железа VFe = 340 W.

Сумма всех потерь

54) Находим к. п. д. при номинальной нагрузке

η =	Р2	=	15	= 0,86.
	Р2 + V		15 + 2,35.