ГЛАВА IV
М. Д. С. ОБМОТОК АСИНХРОННОГО ДВИГАТЕЛЯ
§ 39. Кривая м. д. с. для трехфазной обмотки.
Представим себе статор, в пазах которого размещены три обмотки: I, II, III, смещенные друг относительно друга в пространстве на 120° (фиг. 12). Предположим, что эти три обмотки питаются трехфазным током, так что в какой-нибудь момент времени обмотка I обтекается током, величина которого i1= Im • sin ωt, обмотка II обтекается током i2 = Im • sin (ωt — 120°) и, наконец, обмотка III обтекается током i3 = Im • sin (ωt — 240°).
Токи i1, i2, i3 вызовут в обмотках, или, как их чаще всего называют, "фазах", I, II и III соответственной величины м. д. с. F1, F2, F3.
Предположим для упрощения задачи, что эти три м. д. с. имеют синусоидальное распределение вдоль окружности статора. Амплитуды этих трех синусоид, представляющих кривые м. д. с. во всех трех фазах, в какой-нибудь данный момент времени (t) будут:
F2 = F • sin (ωt — 120°) (фаза II),
F3 = F • sin (ωt — 240°) (фаза III).
Для наглядности вышеприведенные значения м. д. с. и токов зане¬сены в нижеследующую таблицу:
ТАБЛИЦА 7
| № фаз | Ток в фазе | Амплитудное значение м. д. с. данной фазы в данный момент времени | Максимальное значение амплитуды |
| I | i1= Im • sin ωt | F1= F • sin ωt | F |
| II | i2 = Im • sin (ωt — 120°) | F2 = F • sin (ωt — 120°) | F |
| III | i3 = Im • sin (ωt — 240°) | F3 = F • sin (ωt — 240°) | F |
Если бы три синусоиды, имеющие в данный момент времени амплитуды Fl, F2 и F3, совпадали по своему положению в пространстве, то для нахождения результирующей амплитуды Fr мы должны были бы произвести алгебраическое сложение:
Fr = F1 + F2 + F3,
Fr = F • sin ωt + F • sin (ωt — 120°) + F • sin (ωt — 240°) =
= F• [sin ωt + sin (ωt — 120°) + sin (ωt — 240°)].
Произведя необходимые тригонометрические преобразования выражения, стоящего в прямых скобках, мы найдем, что это выражение равно нулю; таким образом мы видим, что в этом случае результирующая величина
Fr = 0.
Случай совпадения осей м. д. с. Fl, F2 и F3, иллюстрирует приведенная выше фиг. 13, где изображен железный сердечник, на котором находятся три катушки I, II и III, обтекаемые трехфазным током; при указанном на фиг. 13 расположении катушек последние в магнитном отношении компенсируют друг друга, так что при такой системе магнитный поток в сердечнике будет равен нулю. В статоре асинхронного двигателя мы имеем другой случай: здесь обмотки всех трех фаз I — II — III смещены в пространстве друг относительно друга на угол 120° (фиг. 12). Амплитуды кривых м. д. с, создаваемых этими обмотками Fl, F2, F3, должны быть также смещены в пространстве друг относительно друга на 120°, как это показывает развернутая диаграмма фиг. 64. На этой диаграмме показаны кривые м. д. с. Fl, F2 и F3 в виде трех синусоид I — II — III всех трех фаз обмотки статора. Мы видим из этой фигуры, что амплитуды этих синусоид I — II — III смещены друг относительно друга на постоянный угол в 120°.
Так как обмотки фаз I — II — III питаются трехфазным током, то величина амплитуд синусоид I — II — III все время изменяется в такт с изменением моментального значения величины переменного тока.
Величины мгновенного значения тех токов, которые питают обмотки фаз I — II — III, даются векторными диаграммами, изображенными справа на фиг. 64. При этом проекция векторов I — II — III на вертикаль в некотором масштабе будет давать нам величины соответственных м. д. с. отдельных фаз.
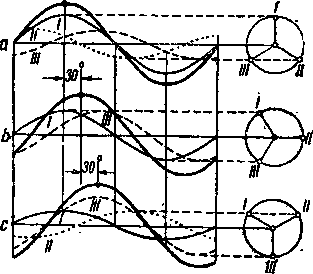 |
| Фиг. 64. Кривые м. д. с. отдельных фаз. |
Для момента времени, соответствующего фиг. 64, а, мы видим, что ток в фазе I, определяемый как проекция вектора I на вертикаль, будет равен амплитудному значению; ток в фазах II и III (равный в некотором масштабе проекциям соответствующих векторов II — III на вертикаль) будет равен половинному значению амплитуды и будет иметь отрицательное направление по сравнению с током, текущим в фазе I. Построим кривые м. д. с. в виде синусоид I, II и III, смещенных друг относительно друга на 120°, имея в виду, что согласно только что сказанному максимальная ордината синусоиды I должна быть равна амплитуде, а максимальные ординаты синусоид II и III должны иметь отрицательное значение и должны равняться половине амплитуды.
Сложив ординаты всех этих синусоид I — II — III, мы получим результирующую кривую, показанную всюду на фиг. 64 жирными линиями. На фиг. 64, b показаны кривые м. д. с. отдельных фаз I — II — III, соответствующие тому моменту, когда при вращении (против стрелки часов) векторов тока I — II — III (фиг. 64, справа) вектор II занимает горизонтальное положение. Находя проекции на вертикаль для этого случая, мы видим, что моментное значение тока в фазе II равно нулю, а токи в фазах I и III имеют противоположное направление, причем величины этих токов составляют 0,866 от амплитудного значения.
Между результирующими кривыми фиг. 64, а и b существует разность фаз по времени, соответствующая повороту векторов I — II — III на 30°, что в свою очередь соответствует 1/12 периода. На фиг. 64, с показаны такие же графические построения для другого момента времени, причем каждый момент времени отличается от другого предыдущего на 1/12 часть периода.
Сравнивая части фиг. 64 между собой, мы можем констатировать следующие два явления:
1. Амплитуда результирующей синусоиды все время сохраняет постоянной свою величину (как будет видно из дальнейшего, амплитуда этой результирующей синусоиды при т = 3 составляет 1,5 от амплитуды каждой отдельной синусоиды).
2. Амплитуда результирующей кривой все время перемещается в пространстве таким образом, что она располагается вдоль оси той фазы, которая в данный момент времени обтекается максимальным током.
