ГЛАВА XXXVI
МАГНИТНЫЕ ПОТОКИ РАССЕЯНИЯ
§ 325. Расчет рассеяния торцевых или лобовых частей обмоток.
Сначала рассмотрим фазные обмотки. Потоки рассеяния, создаваемые лобовыми частями таких обмоток, замыкаются в воздушном пространстве, окружающем торцевые части, причем на величину этих потоков оказывает влияние не только тип и конструкция обмоток, но также и близость железных масс.
Ввиду того что пути линий рассеяния вокруг головок обмоток не могут быть точно определены, приходится довольствоваться приближенными расчетными формулами, включающими в себя эмпирические коэфициенты.
Величина удельной магнитной проводимости лобовых частей секции может быть подсчитана по следующей формуле:
| λs = | ls | qs λв . |
| li |
В этой формуле означают:
ls — средняя длина лобовых частей одной полусекции;
qs — число головок, объединенных в одну группу с торца;
λв— удельная магнитная проводимость потока рассеяния для частей секции, расположенных вне паза (лобовые части обмотки). Принимая приближенно λв ≈ 0,4π • 0,4 = 0,5 и ls = 1,5τ, найдем
| λs = | 1,5τqs • 0.5 | ≈ 0,70 | τqs | . |
| li | li |
Для однослойной катушечной двухплоскостной обмотки следует подставить в вышенаписанную формулу qs = q, после чего получим
λs = 0,7τq/li .
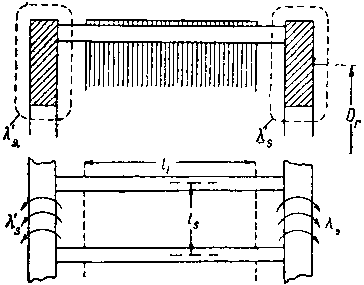 |
| Фиг. 347. Потоки рассеяния вокруг торцевых колец беличьей клетки. |
Для однослойной катушечной обмотки с торцевыми частями, изогнутыми в трех плоскостях (так называемая трехплоскостная или "трехэтажная" обмотка), следует в формулу (325,1) подставить qs = q/2, после чего получится
λs ≈ 0,4τq/li .
Для двухслойной ("американской") обмотки можно применить ту же вышенаписанную формулу:
λs ≈ 0,4τq/li .
Теперь обратимся к беличьей обмотке и попытаемся найти удельную магнитную проводимость λ's потоков рассеяния, замыкающихся вокруг торцевых колец, как показано на фиг. 347.
Найдем приведенную к длине ротора li величину удельной магнитной проводимости
| λs = | ls | • λ's |
| li |
Находим
| ls = | πDr | . |
| z2 |
где Dr — диаметр средней окружности замыкающего кольца и N2— общее число стержней беличьей обмотки (фиг. 347). Принимая приближенно величину λ's ≈0,8, найдем
| λs = | 2πDr | 0,8; |
| z2li |
| λs = 2,5 | Dr | . |
| z2li |
