АСИНХРОННЫЕ
МАШИНЫ

ГЛАВА XXXII
РАСЧЕТ АСИНХРОННОГО ДВИГАТЕЛЯ

§ 278.   Физический   смысл   постоянной   С;   удельное    тяговое усилие.

Полученное выше основное уравнение

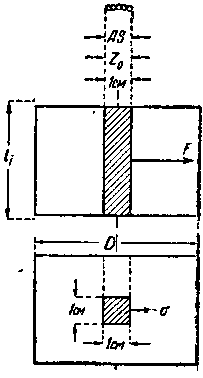Фиг. 326. Удельное тяговое

D2 • li • n1	=	5,5 • 1011	,
kVA		k1αiBlAS

можно переписать в таком виде

D2 • li • n1	=	5,5 • 1011	,
kVA		σ

Величина σ = k1αiBlAS, входящая в знаменатель вышенаписанного выражения, имеет вполне определенный физический смысл.

Постараемся его здесь раскрыть. Для этой цели на внешней цилиндрической рабочей поверхности ротора по всей его длине li вырежем мысленно полоску шириной в 1  cm (фиг. 326).

Предположив, что наша машина работает двигателем, найдем то усилие F, с которым пучок проводов, расположенных на внешней цилиндрической поверхности ротора на протяжении 1 cm части окружности, будет стремиться перемещаться под воздействием магнитного поля Вl.

Если бы сдвиг фаз между током ротора и э. д. с., наводимой в роторе вращающимся потоком, отсутствовал, т. е. ψ = 0, то мы бы могли написать

где Ia — ток в проводе ротора;

Z0 — число проводов, расположенных на длине в 1 cm окружности ротора.

Произведение IaZ0 представляет собой число ампервитков, прихо­дящееся на 1 cm длины окружности ротора, и равно линейной нагрузке AS.

Поэтому вышенаписанное выражение получит следующий вид:

Теперь найдем то тяговое усилие σ, которое будет приложено к одному квадратному сантиметру рабочей поверхности ротора (фиг. 326, нижний чертеж).

Это усилие σ будет меньше, чем F в отношении li, т. е. мы получим

Подставляя  сюда Вс  = αiBl найдем

khkkgkggkgkg

В этой формуле должно быть учтено влияние коэфициента k1:

Формула (278,2) написана в предположении, что угол сдвига фаз
φ = 0.

Если этот угол не равен нулю, то следует написать

В дальнейшем, однако, в расчет всюду будем вводить формулу (278,2), имея в виду некоторую фиктивную или "кажущуюся" величину удельного тягового усилия, соответствующую кажущейся мощности машины, измеряемой в kVA.

Заметим,  что приближенно в среднем можно положить положить

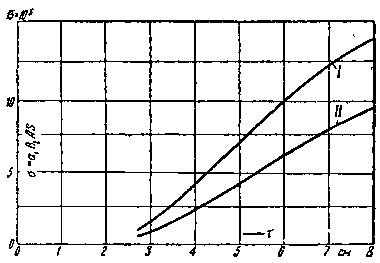Фиг. 328. Удельное  тяговое  усилие σ в функции τ.

Поэтому кажущуюся величину удельного тягового усилия часто приближенно можно подсчитывать по более простой формуле:

На фиг. 327 и 328 показаны кривые зависимости σ от величины полюсного деления τ. Из этих фигур видно, что при возрастании τ растет σ, т. е. коэфициент использования машины увеличивается.

Кривые   I   фиг.    327-328 относятся   к  сильно использованным машинам с усиленной вентиляцией. 1 В случае открытых, вентилируемых (но без форсировки)   машин   можно   пользоваться кривыми II на фиг. 327—328. Этими же кривыми можно пользоваться при расчете двухполюсных машин.

Обмоточный   коэфициент k1, входящий  в уравнение  (278,2),   может быть представлен как произведение

где kp — коэфициент, учитывающий влияние распределения обмотки в пазах, и

ky — коэфициент, учитывающий влияние укорочения шага обмотки.

В среднем можно принять для трехфазной обмотки k1 ≈ 1. В этом случае

D2 • li • n1	=	5,5 • 1011	,
kVA		αiBlAS

Кажущаяся мощность, потребляемая двигателем из сети в киловольтамперах, связана с полезной мощностью на валу двигателя в киловаттах следующим соотношением:

kVA =	kW	,
	η cos φ

Подставляя последнее в вышенаписанное, получим