§ 42. М. д. с. равномерно распределенной трехфазной обмотки.

В предыдущих параграфах мы изучали м. д. с. синусоидальной формы. В действительности эти кривые в большей или меньшей степени отличаются от синусоидальных кривых.

Фиг. 66. Построение кривой м. д. с. для "гладкой" обмотки.

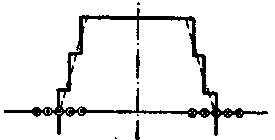
Кривые м. д. с, создаваемые обмотками отдельных фаз, напоминают более или менее ступенчатую форму, изображенную на фиг. 65, где изображена кривая м. д. с. одной фазы, у которой число q равно 5.

С возрастанием числа q число ступеней такой кривой соответственно возрастает, и в пределе кривая м. д. с. получает трапецоидальную форму, изображенную на фиг. 65 пунктиром.

Фиг. 65. Кривая м. д. с. одной фазы
q = 5.

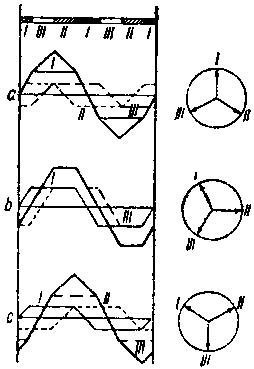
На фиг. 66 дано построение кривой м. д. с. для гладкой трехфазной обмотки (с весьма большим числом q).

Как видно из фиг. 66, форма результирующей м. д. с. при протекании по обмоткам статора I — II — III трехфазного тока все время меняет свою форму с остроугольной (фиг. 66, а) на тупоугольную (фиг. 66, b).

Таким образом амплитуда кривой результирующей м. д. с. не пред ставляет собой постоянной величины, но пульсирует с некоторой частотой.

Из фиг. 66 видно, что кривая м. д. с. переходит из остроугольной формы в тупоугольную каждый раз при повороте векторов на угол в 30° (рис. справа на фиг. 66).

Принимая во внимание, что общий период, в течение которого кривая м. д. с. получает прежнюю форму, равен

2 • 30° = 60°,

убеждаемся, что амплитуда кривой результирующей м. д. с. колеблется с частотой, соответствующей отношению 360/60, т. е. с шестикратной частотой сети.

Величина амплитуды м. д. с. в момент времени, соответствующий фиг. 66, а (остроугольная форма), будет:

Fmax =	√2 • I • q • sn	+ 2 • 0.5 •	√2 • I • q • sn	= √2 • I • q • sn .
	2		2

В момент времени, соответствующий фиг, 66, b (тупоугольная форма), амплитуда м. д. с. будет несколько меньше:

F'max =	√2 • I • q • sn • cos30°	+ 2 • 0.5 •	√2 • I • q • sn• cos30°	= 0.866 •√2 • I • q • sn .
	2		2

Обе амплитуды относятся друг к другу, как

Fmax	=	1	= 1.151.
F'max		0.866

1 Это значит, что амплитуда кривой м. д. с. колеблется примерно в пре-делах 15% около своего среднего значения.

Средняя величина м. д. с. будет

Fср =	Fmax + F'max	=	1 + 0.866	• √2 • I • q • sn = 0.933 •√2 • I • q • sn .
	2		2

или

(42.1)

Fcp = l,32 • I • q • sn.

Выше нами было получено следующее значение для амплитуды первой гармонической м. д. с.:

(42.2)

Fr = 0,45 • т • I • q • sn • k;

для т = 3 это уравнение получит вид:

Fr = 0,45 • 3 • I • q • sn • k;

(42.2')

Fr = 1,35 • I • q • sn • k.

Сравнивая (42,1) с (42,2'), мы видим, что средняя амплитуда для случая гладкой обмотки почти не отличается от амплитуды первой

Оглавление

Вперед

[an error occurred while processing this directive]

АСИНХРОННЫЕ МАШИНЫ

ГЛАВА IV М. Д. С. ОБМОТОК АСИНХРОННОГО ДВИГАТЕЛЯ

§ 42. М. д. с. равномерно распределенной трехфазной обмотки.

АСИНХРОННЫЕ
МАШИНЫ

ГЛАВА IV
М. Д. С. ОБМОТОК АСИНХРОННОГО ДВИГАТЕЛЯ