ГЛАВА XXI
ОДНОФАЗНЫЕ АСИНХРОННЫЕ ДВИГАТЕЛИ. ТЕОРИЯ ВРАЩАЮЩИХСЯ В ПРОТИВОПОЛОЖНЫЕ СТОРОНЫ ПОЛЕЙ
§ 203. Крутящий момент однофазного двигателя.
 |
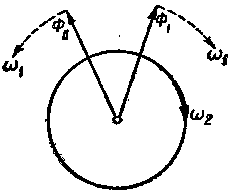 |
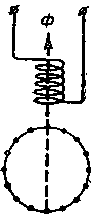
| Фиг. 220. Однофазный двигатель. | Фиг. 221. Разложение пульсирующего потока на два вращающиеся в разные стороны потока. |
Если ротор однофазного асинхронного двигателя неподвижен, то "прямое" и "инверсное" поля, взаимодействуя с токами ротора, развивают равные и противоположные моменты вращения, которые взаимно уничтожаются.
Таким образом мы видим, что начальный момент вращения однофазного асинхронного двигателя равен нулю.
Предположим, что ротор нашего однофазного двигателя посторонним усилием приведен во вращение, например, в сторону вращения стрелки часов (фиг. 221) и вращается со скоростью, немного меньшей синхронной, например, с угловой скоростью:
ω2 = ω1 — s • ω1 = ω1(1— s),
где ω1 = 2πf1— угловая скорость переменного тока, подводимого к статору.
При этом магнитное поле, вращающееся в ту же сторону, что и ротор (т. е. "прямое" поле ФI), вызовет в роторе э. д. с. E2, которая в свою очередь послужит причиной появления токов I2, частота которых будет соответствовать скольжению ротора относительно поля ФI и будет, следовательно, равна s • f1. Этот ток I2, взаимодействуя с "прямым" потоком Ф1, создаст момент вращения
MI = c • ФI • I2 • cos φ2,
Другое поле — "инверсное" — ФII вызовет в роторе токи I3 с частотою I3 = (2 - s)f1 1.
Взаимодействие токов I3 с "инверсным" полем ФII послужит причиной появления момента вращения МII, величина которого будет
MII = c • ФII • I3 • cos φ3,
Результирующий момент двигателя будет равен разности
М = МI — МII.
При неподвижном роторе будет МI = МII; поэтому результирующий момент при этих условиях будет равен нулю.
При вращающемся роторе моменты МI и МII не равны друг другу и, следовательно, не компенсируют друг друга; причина этого заключается в следующем:
"Инверсное" поле ФII наводит токи в роторе значительно большей частоты, чем "прямое" поле ФI.
Например, если скольжение будет равно s = 0,02 (т. е. 2%), то число периодов тока I3, наведенного "прямым" потоком ФI, будет
f1 • s = 50 • 0,02= 1Hz
(2 — s)f1 = (2 — 0,02) • 50 = 99 Hz.
На фиг. 223 изображена векторная диаграмма э. д. с. и токов, вызываемых инверсным полем ФII.
1 Действительно, предположим, что ротор двухполюсного двигателя будет вращаться по стрелке часов со скоростью, несколько меньше синхронной и равной ω2 = (1 — s) ω1, где s— скольжение и ω1 — синхронная угловая скорость.
Тогда относительная скорость пересечения потоком проводников ротора для "прямого" поля будет равна разности
ω1— ω2 = ω1 — (1 — s) • ω1= s • ω1
ω3 = ω1 + ω2 = ω1 + (1 — s)ω1 = ω1(2 — s).
Как видно из этой фигуры, э. д. с. E3, создаваемая инверсным полем ФII, отстает от него на угол в 90°.
Ввиду того что частота f3 э. д. с. E3, наведенной инверсным полем, относительно велика, реактанц ротора, соответствующий этой частоте f3, будет также велик; вследствие этого ток I3, создаваемый э. д. с. Е3, будет отставать по фазе от Е3 на угол φ3, близкий к 90°.
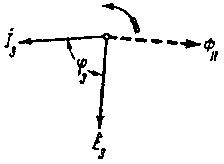 |
| Фиг. 223. |
Таким образом из фиг. 223 мы видим, что вектор тока I3 почти противоположен по фазе относительно потока ФII; отсюда следует, что ток I3 действует размагничивающим образом по отношению к потоку ФII.
В результате под воздействием тока I3 "инверсный" поток будет почти целиком сдемпфирован, и следовательно, поток ФII при вращении ротора почти совсем исчезнет.
Имея в виду на основании сказанного выше, что величина потока ФII будет невелика и что угол сдвига фаз φ2 будет велик, мы убеждаемся, что величина "инверсного" момента на основании формулы (203,2) должна получиться очень небольшой, так что
МII ≈ 0 .
Следовательно, в этом случае вращающегося двигателя результирующий момент будет
М ≈ МI.
