АСИНХРОННЫЕ
МАШИНЫ

ВВЕДЕНИЕ

§ 4. Вращающееся магнитное поле (двухфазное).

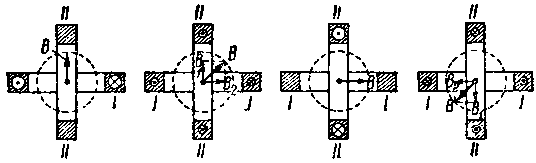
Для того чтобы понять механизм образования вращающегося магнитного поля, рассмотрим следующий примитивный опыт согласно  фиг. 9,b.

На этой фигуре изображены две с одинаковым числом витков катушки I и II, оси которых расположены в пространстве перпендикулярно друг к другу. Как видно из этой фигуры, катушка I обтекается током i1 ,а катушка II — током i2 .

Фиг. 9. Образование вращавшегося двухфазного магнитного поля.

Предположим сначала, что токи i1 и i2 — постоянны и что ток i1 , проходящий по катушке I, создает внутри этой катушки магнитную индукцию В1 , а ток, текущий в катушке II, — индукцию В2 (фиг. 9,а).

Результирующая величина магнитной индукции В в точке О получится путем геометрического суммирования отдельных величин В1 и В2 , согласно фиг.   9,а.

Как видно из этой фигуры, угол наклона а зависит от относительной величины векторов В1 и В2 ; угол α будет сохранять постоянную величину при постоянном значении векторов В1 и В2 .

Теперь посмотрим, что получится, если токи i1 и i2 , питающие катушки I и II, будут переменными.

Предположим вначале, что катушки будут питаться двухфазным током, так что ток в катушке I будет

а в катушке II

Тогда в какой-нибудь момент времени магнитная индукция в середине первой катушки будет

и во второй где В — некоторое амплитудное значение.

Результирующая величина В12 получится путем геометрического сложения векторов В1 и В2 :

Таким образом мы видим, что результирующий вектор В12, полученный путем геометрического сложения двух переменных векторов В1 и В2 , остается все время постоянным:

Посмотрим, как будет при этом меняться его направление, определяемое углом α на фиг. 9, а.

Из прямоугольного треугольника (фиг. 9, а), имеем

tg α =	B2	=	Bm sin(ωt - π/2)	=	sin(ωt - π/2)	=	sin(ωt - π/2)	= tg(ωt - π/2).
	B1		Bm sinωt		sinωt		cos(ωt - π/2)

Фиг. 10. Вращение результирующего вектора В.

Отсюда мы видим, что

т. е. мы видим, что угол α меняется прямо пропорционально времени t.

Таким образом α на фиг. 9,а с течением времени непрерывно возрастает, т. е. это значит, что результирующий вектор В12 вращается с равномерной угловой скоростью, равной со, причем конец этого вектора В12 описывает окружность (фиг. 9,а), в результате чего получается вращающееся магнитное поле.

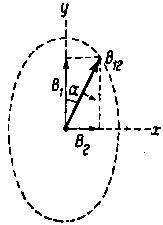Фиг. 11. Эллиптическое вращающееся магнитное поле

На фиг. 10 показано геометрическое построение для разных моментных значений магнитных индукций В1 и В2 , причем моментное значение тока, текущего в катушках I и II, показано условно кружками разного диаметра, Как видно из фиг. 10, результирующий вектор В при обтекании катушки I и II двухфазным током, вращается в пространстве с постоянной скоростью.

Все приведенные выше выводы были сделаны в предположении, что число витков в катушках I и II и эффективное значение напряжений на зажимах этих катушек одинаковы. Если числа витков в катушках I и II неодинаковы, то можно доказать, что конец результирующего вектора В12 будет перемещаться не по окружности, а по эллипсу, в этом случае получается так называемое   эллиптическое  вращающееся магнитное поле (фиг.   11).