ГЛАВА IV
М. Д. С. ОБМОТОК АСИНХРОННОГО ДВИГАТЕЛЯ
§ 43. Многоугольник Гергеса.
Очень интересный и наглядный метод построения кривой м. д. с. в свое время был предложен Гергесом.
Этот метод в общих чертах заключается в следующем:
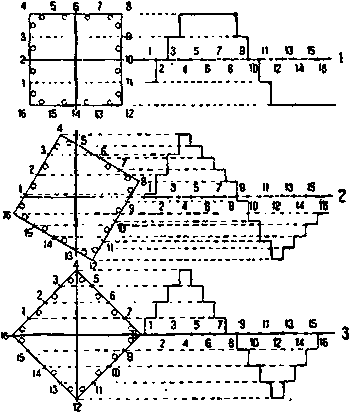 |
| Фиг. 67. Построение кривой м. д. с. для двухфазного двигателя (q = 4). |
Необходимо начертить правильный многоугольник, имеющий 2m сторон, где m — число фаз. Таким образом при двухфазной системе мы получим квадрат и при трехфазной системе правильный шестиугольник.
Затем следует на каждой из сторон многоугольника в виде точек показать пазы — по q пазов на каждой стороне многоугольника, где q— число пазов, приходящееся на полюс и фазу. При этом необходимо наблюдать за тем, чтобы пазы не занимали вершин многоугольника.
Вращая многоугольник и проектируя отдельные точки многоугольника по середине между пазами на вертикаль, мы получим кривую распределения магнитной индукции в разные моменты времени.
На фиг. 67 дано построение кривой м. д. с. для двухфазного двигателя (для q = 4). Положение верхнего квадрата соответствует тому моменту времени, когда ток в одной фазе достиг максимального значения, а в другой фазе равен нулю.
Проводя горизонтали через точки многоугольника 1 — 2— 3, соответствующие отдельным зубцам машины, мы найдем в пересечении с вертикалями, восставленными в точках 1 — 2— 3... справа, соответственные значения величин магнитной индукции.
Повернув квадрат на 45° против стрелки часов, найдем по такому же методу кривую распределения магнитной индукции для того момента, когда мгновенные значения токов в обеих фазах равны друг другу (нижний чертеж фиг. 67). На среднем чертеже фиг. 67 дано построение для момента времени, на 1/12 периода позже по сравнению с верхним чертежом.
Из сравения отдельных кривых фиг. 67 видим, что форма кривой м. д. с. по мере ее передвижения в пространстве (на фиг. 67 справа налево) все время непрерывно меняется, амплитуда этой кривой колеблется, форма кривой постепенно переходит из остроугольной в тупоугольную, причем симметрия кривой по временам нарушается.
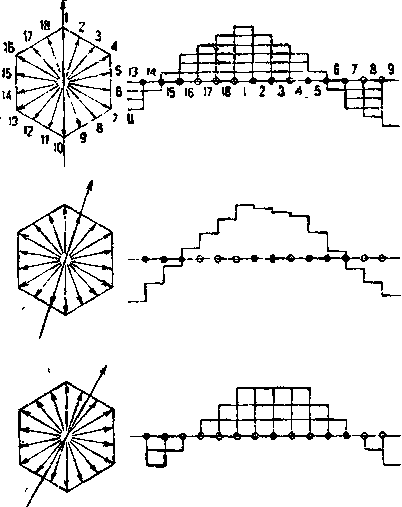 |
| Фиг. 68. Построение кривой м. д. с. для трехфазной обмотки (q = 3). |
На фиг. 68 дано построение кривой м. д. с. по вышеописанному методу Гергеса для трехфазной обмотки с q = 3. Для этого примера мы имели на пару полюсов число зубцов, равное 2mq — = 2 • 3 • 3 = 18. При числе фаз т = 3 полигон Гергеса будет представлять правильный шестиугольник.
Вместо вращения вышеупомянутого шестиугольника против стрелки часов для построения кривой м. д. с. мы можем этот шестиугольник оставить неподвижным и вращать ось времени по стрелке часов, как показано на фиг. 68. На этой фигуре точками 1 — 2 — 3... обозначено положение зубцов, а не пазов, в противоположность фиг. 67.
Справа на фиг. 68 показаны кривые м. д. с, построенные по этому методу для разных моментов времени. Сравнивая эти кривые между собой, мы видим, что форма кривой м. д. с. здесь непрерывно меняется, переходя от остроугольной формы к тупоугольной и наоборот.
Сравнивая кривые м. д. с. на фиг. 68 и 67, мы видим, что при трехфазном токе форма кривой м. д. с. получается более совершенной в смысле приближения к синусоиде.
В случае же двухфазного тока кривая м. д. с. получает весьма искаженную форму, как видно из фиг. 67.
В этом заключается одно из многих преимуществ трехфазного тока по сравнению с двухфазным.
